КОНТРОЛЬНА РОБОТА ЗА І СЕМЕСТР

ВАРІАНТ 1

Завдання 1 Знайдіть сторону квадрата, якщо його периметр дорівнює 24 см.

Р = 4а, де а – довжина сторони квадрата.

а = Р : 4 = 24 см : 4 = 6 см

A 4 см            Б 6 см

B 8 см            Г 12 см

Завдання 2 На малюнку А₁В₁ || А₂В₂, ОВ₁ = В₁В₂, ОА₁ = 6 см. Знайдіть ОА₂.

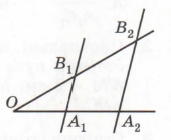
За теоремою Фалеса ОА₁ = А₁А₂.

ОА₂ = ОА₁ + А₁А₂ (основна властивість вимірювання відрізків)

ОА₂ = 2ОА₁ = 2 • 6 см = 12 см

A Знайти неможливо   Б 10 см

B 6 см                         Г 12 см

 

Завдання 3   За яких з наведених умов ∆KLM і ∆K₁L₁M₁ подібні?

Відповідні кути повинні бути рівними ∠К = ∠К₁, ∠L = ∠L₁, ∠M = ∠M₁.

Якщо ∠K = ∠K₁ = 25°, то інші відповідні кути не обов’язково будуть рівними.

Якщо ∠K = ∠K₁, ∠L = 30°, ∠L₁ = 35°, то відповідні кути ∠L ≠ ∠L₁, оскільки сума кутів дорівнює однаковому числу.

Якщо ∠L = ∠L₁, ∠M = 29°, ∠M₁ = 29°, два відповідні кути рівні, тоді треті відповідні кути також рівні, оскільки сума кутів трикутника однакове число.

Якщо ∠M = ∠M₁, ∠K = 120°, ∠L₁ = 120°, оскільки у трикутнику не може бути двох тупих кутів, відповідні кути ∠K ≠ ∠K₁.

A ∠K = ∠K₁ = 25°

Б ∠K = ∠K₁, ∠L = 30°, ∠L₁ = 35°

B ∠L = ∠L₁, ∠M = 29°, ∠M₁ = 29°

Г ∠M = ∠M₁, ∠K = 120°, ∠L₁ = 120°

  

Завдання 4 ABCD – ромб, ∠ABD = 50°. Знайдіть ∠A.

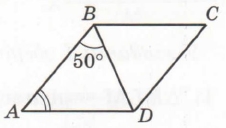
АВ = СD (за означенням ромба), звідси ∆АВD – рівнобедрений,   

∠АВD = ∠ВDА (властивість про кути про основі рівнобедреного трикутника).

∠А = 180° – (∠АВD + ∠ВDА) = 180 – (50° + 50°) = 80° (за теоремою про суму кутів трикутника).

A 80°        Б 40°

B 60°        Г 70°

 

Завдання 5 Основа рівнобедреного трикутника дорівнює 6 см, а бічна сторона – 8 см. Знайдіть периметр трикутника, вершинами якого є середини сторін цього трикутника.

Середня лінія трикутника дорівнює половині паралельної сторони.

6 см : 2 = 3 см – основа утвореного трикутника.

8 см : 2 = 4 см – кожна бічна сторона утвореного трикутника. 

Р = 4 см + 3 см + 4 см = 11 см

A 10 см       Б 11 см

B 12 см       Г 14 см

 

Завдання 6 Катет прямокутного трикутника дорівнює 6 см, а його проекція на гіпотенузу – 4 см. Знайдіть гіпотенузу трикутника.

Позначимо катет буквою а, гіпотенузу – с, то проекція цього катета на гіпотенузу – с_а. За умовою катет а = 6 см, проекція на гіпотенузу с_а = 4 см.

Катет прямокутного трикутника є середнім пропорційним гіпотенузи та проекції цього катета на гіпотенузу.

а² = с • с_а  (теорема про пропорційні відрізки у прямокутному трикутнику).

Гіпотенуза с = а² : с_а = 6² : 4 = 36 : 4 = 9 (см)

A 9 см         Б 10 см

B 8 см          Г 12 см

 

Завдання 7 У прямокутній трапеції гострий кут дорівнює 60°, більша бічна сторона – 10 см , а більша основа – 9 см. Знайдіть меншу основу трапеції.

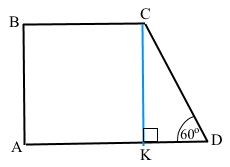
Дано трапеція ABCD – прямокутна, ∠А = ∠В = 90°, ∠D = 60°, CD = 10 см, АD = 9 см.

Проведемо з вершини С висоту СК до основи АD, ∆КСD – прямокутний, ВС = АК.

∠КСD = 90° – 60° = 30° (теорема про суму кутів прямокутного трикутника).

КD = 12 СD = 102 = 5 (см) (катет напроти кута 30°).

 

АD = АК + КD = ВС + КD,

звідки ВС = АD – КD = 9 – 5 = 4 (см)

Відповідь: 4 см.

A З см        Б 4 см

B 5 см        Г 6 см

Завдання 8 Пряма KL паралельна стороні ВС трикутника ABC. ВС = 12 см, KL = 8 см, KB = 2 см. Знайдіть довжину сторони АВ.

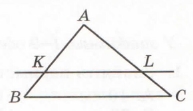
За умовою пряма КL || ВС, то ∆BAC ~ ∆KAL (лема про пряму, паралельну стороні трикутника).

Складемо відношення для сторін подібних трикутників:

ABAK = ACAL = BCKL

Підставимо значення довжин:

ABAK = ACAL = 128

ABAK = 128

8АВ = 12АК  

Врахуємо АК = АВ – ВК = АВ – 2 см (за основною властивістю вимірювання відрізків).  

8АВ = 12(АВ – 2)

Нехай х (см) – сторона АВ. Маємо рівняння.  

8х  = 12 • (х – 2)

8х = 12х – 24

24 = 12х – 8х

4х = 24

х = 24 : 4

х = 6 (см) – сторона АВ.

A 10 см        Б 8 см

B 4 см          Г 6 см

Завдання 9 Бісектриса кута А паралелограма ABCD ділить сторону ВС на від­різки ВК і КС так, що ВК : КС = 1:2. Знайдіть ВС, якщо пери­метр паралелограма дорівнює 80 см.

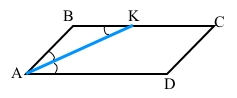
За умовою АВСD – паралелограм (АD || ВС), АК – бісектриса кута А (∠ВАК = ∠DАК).

Бісектриса АК є січною прямих АD || ВС, то різносторонні внутрішні кути ∠ВКА = ∠DАК.  Тому ∠ВКА = ∠ВАК, ∆АВК – рівнобедрений (ознака за двома рівними кутами), АВ = ВК.

BC = BK + KC.

Р = 2(АВ + ВС)

Нехай х (см) – сторона АВ, х + 2х (см) – сторона ВС. Маємо рівняння.

2(х + (х + 2х)) = 80

х + (х + 2х) = 80 : 2

4х = 40

х = 40 : 4

х = 10

х + 2х = 10 + 2 • 10 = 30 (см) – довжина сторони ВС.

А 10 см      Б 20 см       В 30 см     Г 15 см

Завдання 10 У прямокутнику ABCD діагоналі перетинаються в точці О. Кут ОАВ на 30° менший від кута АОВ. Установіть відповід­ність між кутами та їхніми градусними мірами.

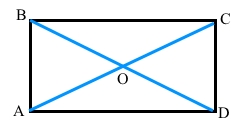
Дано АВСD – прямокутник, ВD = АС = 2ВО = 2АО (діагоналі рівні та точкою перетину діляться пополам), звідси ВО = АО, ∆ОАВ – рівнобедрений, ∠ОВА = ∠ОАВ (властивість кутів рівнобедреного трикутника).

∠ОАВ + ∠ОВА + ∠АОВ = 180° (теорема про суму кутів трикутника),

2∠ОАВ + ∠АОВ = 180°.

Нехай х (°) – міра кута АОВ, х – 30 (°) – міра ОАВ. Маємо рівняння рівняння.    

2(х – 30) + х = 180

2х – 60 + х = 180

3х – 60 = 180

3х = 180 + 60

3х = 240

х = 240 : 3

х = 80 (°) – ∠АОВ.

х – 30 = 80 – 30 = 50 (°) – ∠ОАВ, ∠АВО.

Точка О є BD, звідси ∠АВО = ∠АВD. Розглянемо ∆АВD – прямокутний (∠А = 90°).

∠ВDА = 90° – ∠АВD = 90° – 50° = 40° (наслідок про суму кутів прямокутного трикутника).

1 ∠OAB ——> B 50°

2 ∠AOB ——> Г 80°

3 ∠BDA ——> Б 40°

 

ВАРІАНТ 2

Завдання 1 Знайдіть периметр квадрата, сторона якого дорівнює 5 см.

Р = 4а, де а – довжина сторони квадрата.

Р = 5 см • 4 = 20 см

A 10 см      Б 15 см

B 20 см      Г 25 см

Завдання 2 На малюнку А₁В₁ || А₂В₂, ОА₁ = А₁А₂, ОВ₂ = 6 см. Знайдіть ОВ₁.

За теоремою Фалеса ОВ₁ = В₁В₂.

ОВ₂ = ОВ₁ + В₁В₂ (основна властивість вимірювання відрізків)

ОВ₂ = 2ОВ₁

ОВ₁ = ОВ₂/2 = 6/2 см = 3 см

A б см        Б 4 см

B З см        Г 8 см

Завдання 3  За яких з наведених умов ∆BCD і ∆B₁C₁D₁ подібні?

Відповідні кути повинні бути рівними ∠B = ∠B₁, ∠C = ∠C₁, ∠D = ∠D₁.

Якщо ∠В = ∠В₁ = 45°, то інші відповідні кути не обов’язково будуть рівними.

Якщо ∠В = ∠В₁, ∠С = 50°, ∠С₁ = 50°, два відповідні кути рівні, тоді треті відповідні кути також рівні, оскільки сума кутів трикутника однакове число.

Якщо ∠C = ∠C₁, ∠B = 110°, ∠D₁ = 110°, оскільки у трикутнику не може бути двох тупих кутів, відповідні кути ∠B ≠ ∠B₁.

Якщо ∠D = ∠D₁, ∠B = 43°, ∠B₁ = 42°, то відповідні кути  ∠C ≠ ∠C₁, оскільки сума кутів дорівнює однаковому числу.   

А  ∠В = ∠В₁ = 45°

Б  ∠В = ∠В₁, ∠С = 50°, ∠С₁ = 50°

В  ∠C = ∠C₁, ∠B = 110°, ∠D₁ = 110°

Г  ∠D = ∠D₁, ∠B = 43°, ∠B₁ = 42°

Завдання 4 ABCD – ромб,  ∠D = 40°. Знайдіть ∠DAC.

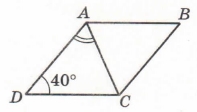
DА = DС (за означенням ромба), звідси ∆СDА – рівнобедрений,

∠DАС = ∠АСD (властивість про кути про основі рівнобедреного трикутника).

∠DАС = (180° – ∠D) : 2 = (180° – 40°) : 2  = 70° (за теоремою про суму кутів трикутника).

A 80°      Б 50°

B 60°      Г 70°

Завдання 5 Бічна сторона рівнобедреного трикутника дорівнює 6 см, а осно­ва - 10 см. Знайдіть периметр трикутника, вершинами якого є се­редини сторін цього трикутника.

6 см : 2 = 3 см – довжина бічної сторони утвореного рівнобедреного трикутника.

Основа утвореного трикутника лежить на середній лінії трикутника, звідси

10 см : 2 = 5 см – основа утвореного рівнобедреного трикутника.

Р = 3 см + 5 см + 3 см = 11 см

A 10 см        Б 11 см

B 12 см        Г 13 см

Завдання 6 Катет прямокутного трикутника дорівнює 4 см, а його проекція на гіпотенузу – 2 см. Знайдіть гіпотенузу трикутника.

Позначимо катет буквою а, гіпотенузу – с, то проекція цього катета на гіпотенузу – с_а. За умовою катет а = 4 см, проекція на гіпотенузу с_а = 2 см.

Катет прямокутного трикутника є середнім пропорційним гіпотенузи та проекції цього катета на гіпотенузу.

а² = с • с_а  (теорема про пропорційні відрізки у прямокутному трикутнику).

Гіпотенуза с = а² : с_а = 4² : 2 = 16 : 2 = 8 (см)

A б см       Б 9 см

B 8 см       Г 10 см

Завдання 7 У прямокутній трапеції гострий кут дорівнює 60°, більша бічна сторона – 12 см, а менша основа – 5 см. Знайдіть більшу основу трапеції.

Дано трапеція ABCD – прямокутна, ∠А = ∠В = 90°, ∠D = 60°, CD = 12 см, ВС = 5 см.

Проведемо з вершини С висоту СК до основи АD, ∆КСD – прямокутний, ВС = АК.

∠КСD = 90° – 60° = 30° (теорема про суму кутів прямокутного трикутника).

КD = 12 СD = 122 = 6 (см) (катет напроти кута 30°).

АD = АК + КD = ВС + КD = 5 + 6 = 11 (см)

Відповідь: 11 см.

A 9 см       Б 10 см

B 11 см      Г 12 см

Завдання 8 Пряма MN паралельна стороні АС трикутника ABC. АС = 9 см, MN = 3 см, AM = 4 см. Знайдіть довжину сторони АВ.

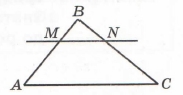
За умовою пряма MN || AC, то ∆MBN ~ ∆ABC (лема про пряму, паралельну стороні трикутника).

Складемо відношення для сторін подібних трикутників:

ABMB = ACMN = BCBN

Підставимо значення довжин:

ABMB = 93

ABMB = 93 = 3

ABMB = 3

АВ = 3MB  

Врахуємо MB = АВ – AM = АВ – 4 см (за основною властивістю вимірювання відрізків). 

AB = 3(АВ – 4)

Нехай х (см) – сторона АВ. Маємо рівняння. 

х  = 3(х – 4)

х = 3х – 12

12 = 3х – х

2х = 12

х = 12 : 2

х = 6 (см) – сторона АВ.

A 5 см          Б 8 см

B 7 см          Г 6 см

Завдання 9 Бісектриса кута В паралелограма ABCD ділить сторону AD на від­різки AM і MD так, що AM : MD = 1:3. Знайдіть AD, якщо пери­метр паралелограма ABCD дорівнює 100 см.

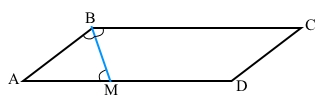
За умовою АВСD – паралелограм (АD || ВС), BК – бісектриса кута B (∠ВАM = ∠CАM).

Бісектриса BК є січною прямих АD || ВС, то різносторонні внутрішні кути ∠ВMА = ∠MBC.  Тому ∠ABM = ∠AMB, ∆АВM – рівнобедрений (ознака за двома рівними кутами), АВ = AM.

AD = AM + MD.

Р = 2(АВ + AD) = 2(AM + AD)

Нехай х (см) – сторона AM, 3x (см) – довжина відрізка MD, х + 3х (см) – сторона AD. Маємо рівняння.

2(х + (х + 3х)) = 100

х + х + 3х = 100 : 2

5х = 50

х = 50 : 5

х = 10

х + 3х = 10 + 3 • 10 = 40 (см) – довжина сторони AD.

А З0 см     Б 40 см     В 45 см      Г 35 см

Завдання 10 У прямокутнику ABCD діагоналі перетинаються в точці О. Кут АОВ на 15° більший за кут АВО. Установіть відповід­ність між кутами та їхніми градусними мірами.

Дано АВСD – прямокутник, ВD = АС = 2ВО = 2АО (діагоналі рівні та точкою перетину діляться пополам), звідси ВО = АО, ∆ОАВ – рівнобедрений, ∠АВО = ∠ВАО (властивість кутів рівнобедреного трикутника).

∠АВО + ∠ВАО + ∠АОВ = 180° (теорема про суму кутів трикутника),

2∠АВО + ∠АОВ = 180°.

Нехай х (°) – міра кута АВО, х + 15 (°) – міра АОВ. Маємо рівняння.    

2х + х + 15 = 180

3х + 15 = 180

3х = 180 – 15

3х = 165

х = 165 : 3

х = (150 + 15) : 3

х = 55 (°) – ∠АВО, ∠ВАО.

х + 15 = 55 + 15 = 70 (°) – ∠АОВ.

У прямокутнику ∠А = 90°, ∠ВАО + ∠САD =∠А (основна властивість вимірювання кутів),

звідси ∠САD = ∠А – ∠ВАО = 90° – ∠ВАО = 90° – 55° = 35°

1 ∠AOB ——> Г 70°

2 ∠ABO ——> Б 55°

3 ∠CAD ——> A 35°