САМОСТІЙНА РОБОТА 5 [11М]

Узагальнена теорема Фалеса. Подібні трикутники. Ознаки подібності трикутників

ВАРІАНТ 1

Завдання 1   ∆АВС – різносторонній, ∆ABC ~ ∆А₁В₁С₁.  Тоді АВA₁B₁
 = …

 

Для подібних трикутників виконується відношення для відповідних сторін:

АВA₁B₁
 = ВСВ₁С₁
 = АСA₁С₁
 

 

А АСA₁С₁
    Б ВСB₁C₁
     B BCA₁C₁
    Г АСВ₁С₁
 

 

Завдання 2 Паралельні прямі AM, BN і СК перетина­ють сторони кута з вершиною О так, що OA = 4 см, АВ = 2 см, ВС = 6 см, ОМ = 5 см. Знайдіть MN і NK.

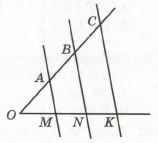
Для паралельних прямих АМ і BN cкладемо відношення відрізків  ОААВ = OMMN (узагальнена теорема Фалеса).

MN = OM • ABOA   = 5 • 24 = 104 = 2,5 (см)

 

Для паралельних прямих BN і CK cкладемо відношення відрізків ОBВC = ОNNK (узагальнена теорема Фалеса).

NK = ON • BCOB

 

OB = OA + AB = 4 см + 2 см = 6 см (основна властивість вимірювання відрізків);

ON = OM + MN = 5 см + 2,5 см = 7,5 см (основна властивість вимірювання відрізків).

NK = 7,5 • 6 : 6 = 7,5 см   

Відповідь: MN = 2,5 см; NK = 7,5 см.  

Завдання 3 Сторони трикутника відносяться як 4 : 5 : 6. Знайдіть невідомі сторони подібного йому трикутника з периметром 45 см.

І — 4х

ІІ — 5х

ІІІ — 6х

Р — 15 х — 45 см

Розв’язання    

Нехай 4х (см) – перша сторона, 5х (см) – друга сторона, 6х (см) – третя сторона, тоді 4х + 5х + 6х (см) – периметр. Маємо рівняння.

4х + 5х + 6х = 45

15х = 45

х = 45 : 15

х = 3

4х = 4 • 3 = 12 (см) – І сторона.

5х = 5 • 3 = 15 (см) – ІІ сторона.

6х = 6 • 3 = 18 (см) – ІІІ сторона.

Відповідь: 12 см, 15 см, 18 см.   

Завдання 4 На стороні АС трикутника ABC вибрано точку М так, що ∠ABM = ∠C. Знайдіть довжину відрізка МС, якщо AM = 2 см, АВ = 4 см.

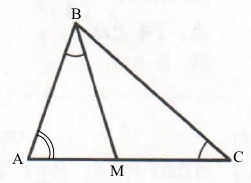
Підказка.

Для трикутника АВС підбираємо слідування відповідних кутів подібного трикутника (від цього залежатиме назва подібного трикутника).  

За умовою ∠С = ∠ABM, кут ∠А – спільний, тоді третя пара відповідних кутів ∠В = ∠ВМА. Для ∆АВС подібним стає ∆АМВ.   

Розв’язання  

За умовою ∠С = ∠ABM, кут ∠А – спільний, трикутники ∆ABC ~ ∆AMB будуть подібними за двома кутами, якщо відповідні сторони пропорційні.

АВАМ  = ВСМВ =  АСАВ

 

Підставимо числові значення.

42 = ВСМВ = АС4

42 = АС4

АС4  = 42

АС = 4 • 42 = 8 (см)

 

Також  АС = АМ + МС (основна властивість вимірювання відрізків).

МС = АС – АМ = 8 см – 2 см = 6 см.  

Відповідь: МС = 6 см.   

ВАРІАНТ 2

Завдання 1 ∆KLM – різносторонній, ∆KLM ~ ∆K₁L₁M₁. Тоді LML₁M₁
 = …

 

Для подібних трикутників виконується відношення для відповідних сторін:

KLK₁L₁ = LML₁M₁ = KMK₁M₁

 

АKLK₁M₁     Б KLM₁L₁    ВKMK₁L₁     Г KMK₁M₁

Завдання 2 Паралельні прямі АК, BL і СМ пере­тинають сторони кута з вершиною О так, що ОК = 3 см, KL = 2 см, LM = 5 см, АВ = 3 см. Знайдіть OA і ВС.

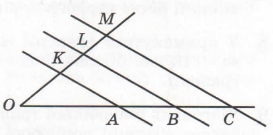
Для паралельних прямих KA і LB cкладемо відношення відрізків OKKL = OAAB (узагальнена теорема Фалеса).

OA = OK • AB KL = 3 • 3 2 = 92 = 4,5 (см)

 

Для паралельних прямих LB і MC cкладемо відношення відрізків OLLM = OBBC (узагальнена теорема Фалеса).

BC = OB • LM OL  

 

OL = OK + KL = 3 см + 2 см = 5 см (основна властивість вимірювання відрізків);

OB = OA + AB = 4,5 см + 3 см = 7,5 см (основна властивість вимірювання відрізків).

BC = 7,5 • 5 5 = 7,5 см  

  

Відповідь: OA = 4,5 см; BC = 7,5 см. 

 

Завдання 3 Сторони трикутника відносяться як 4:5:7. Знайдіть невідомі сторони подібного йому трикутника з пери­метром 32 см.

І — 4х

ІІ — 5х

ІІІ — 7х

Р — 16 х — 32 см

Розв’язання   

Нехай 4х (см) – перша сторона, 5х (см) – друга сторона, 7х (см) – третя сторона, тоді 4х + 5х + 7х (см) – периметр. Маємо рівняння.

4х + 5х + 7х = 32

16х = 32

х = 32 : 16

х = 2

4х = 4 • 2 = 8 (см) – І сторона.

5х = 5 • 2 = 10 (см) – ІІ сторона.

7х = 7 • 2 = 14 (см) – ІІІ сторона.

Відповідь: 8 см, 10 см, 14 см.  

 

Завдання 4 На стороні АВ трикутника ABC вибрано точку F так, що ∠FCB = ∠A, FB = 2 см, ВС = 3 см. Знайдіть довжину відрізка AF.

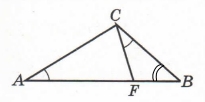
Підказка.

Для трикутника АВС підбираємо слідування відповідних кутів подібного трикутника (від цього залежатиме його назва). 

За умовою ∠A = ∠FCB, кут ∠B – спільний, тоді третя пара відповідних кутів ∠C = ∠CFB). Для ∆АВС подібним стає ∆CBF.  

Розв’язання 

За умовою ∠A = ∠FCB, кут ∠B – спільний, трикутники ∆ABC ~ ∆CBF будуть подібними за двома кутами, якщо відповідні сторони пропорційні.

ABCB = BCBF = ACCF

 

Підставимо числові значення. 

AB3 = 32 = ACCF

AB3 = 32

AB =  3 • 32 = 4,5 (см)

 

АB = АF + FB (основна властивість вимірювання відрізків).

AF = АB – FB = 4,5 см – 2 см = 2,5 см. 

Відповідь: AF = 2,5 см.  

 

ВАРІАНТ 3

Завдання 1  ∆АВС – різносторонній, ∆ABC ~ ∆А₁В₁С₁. Тоді BC/B₁C₁ = …

 

Для подібних трикутників виконується відношення для відповідних сторін:

ABA₁B₁ = BCB₁C₁  =  ACA₁C₁

 

АACA₁C₁     БACB₁C₁     ВABB₁C₁     АABA₁C₁

 

 

Завдання 2 Паралельні прямі АК, ВМ і CN перетинають сторони кута з вершиною О так, що ОК = 4 см, KM = 2 см, MN = 6 см, АВ = 3 см. Знайдіть OA і ВС.

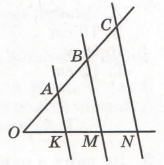
Для паралельних прямих AK і BM cкладемо відношення відрізків OKKM = OAAB (узагальнена теорема Фалеса).

OA = OK • ABKM = 4 • 32 = 122 = 6 (см)

   

Для паралельних прямих BM і CN cкладемо відношення відрізків OMMN = OBBC (узагальнена теорема Фалеса).

BC = OB • MNOM

 

OM = OK + KM = 4 см + 2 см = 6 см (основна властивість вимірювання відрізків);

OB = OA + AB = 6 см + 3 см = 9 см (основна властивість вимірювання відрізків).

BC = 9 • 66 = 9 см  

 

Відповідь: OA = 6 см; BC = 9 см. 

  

Завдання 3 Сторони трикутника відносяться як 5 : 7 : 9. Знайдіть невідомі сторони подібного йому три­кутника з периметром 63 см.

І — 5х

ІІ — 7х

ІІІ — 9х

Р — 21 х — 63 см

Розв’язання   

Нехай 5х (см) – перша сторона, 7х (см) – друга сторона, 9х (см) – третя сторона, то 5х + 7х + 9х (см) – периметр. Маємо рівняння.

5х + 7х + 9х = 63

21х = 63

х = 63 : 21

х = 3

5х = 5 • 3 = 15 (см) – І сторона.

7х = 7 • 3 = 21 (см) – ІІ сторона.

9х = 9 • 3 = 27 (см) – ІІІ сторона.

Відповідь: 15 см, 21 см, 27 см.  

 

Завдання 4 На стороні ВС трикутника ABC вибрано точ­ку К так, що ∠BAK = ∠C. Знайдіть довжину відрізка КС, якщо АВ = 3 см, ВК = 2 см.

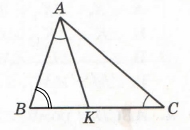
Підказка.

Для трикутника АВС підбираємо слідування відповідних кутів подібного трикутника (від цього залежатиме його назва). 

За умовою ∠C = ∠BAK, кут ∠B – спільний, тоді третя пара відповідних кутів ∠A = ∠AKB). Для ∆АВС подібним стає ∆KBA.  

Розв’язання 

За умовою ∠C = ∠BAK, кут ∠B – спільний, трикутники ∆ABC ~ ∆KBA будуть подібними за двома кутами, якщо відповідні сторони пропорційні.

ABKB = BCBA = ACKA 

 

Підставимо числові значення. 

32 = BC3 = ACKA

32 = BC3

BC = 3 • 32 = 4,5 (см)

 

BC = BK + KC (основна властивість вимірювання відрізків).

KC = BC – BK = 4,5 см – 2 см = 2,5 см. 

Відповідь: KC = 2,5 см.  

 

ВАРІАНТ 4

Завдання 1 ∆KLM – різносторонній, ∆KLM ~ ∆K₁L₁M₁. Тоді KLK₁L₁ = …

 

Для подібних трикутників виконується відношення для відповідних сторін:

KLK₁L₁ = LML₁M₁ = KMK₁M₁

AKMK₁L₁      БLMK₁M₁      ВLML₁M₁          ГKMM₁L₁

   

Завдання 2 Паралельні прямі АК, BL і СМ пе­ретинають сторони кута з верши­ною О так, що OA = 7 см, АВ = 4 см, ВС = 9 см, KL = 2 см. Знайдіть ОК і LM.

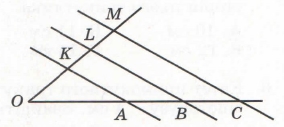
Для паралельних прямих KA і LB cкладемо відношення відрізків OAAB = OKKL (узагальнена теорема Фалеса).

OK = OA • KLAB = 7 • 24 = 144 = 3,5 (см)

Для паралельних прямих LB і MC cкладемо відношення відрізків OBBC = OLLM (узагальнена теорема Фалеса).

LM = OL • BCOB  

 

OB = OA + AB = 7 см + 4 см = 11 см (основна властивість вимірювання відрізків);

OL = OK + KL = 3,5 см + 2 см = 5,5 см (основна властивість вимірювання відрізків).

LM =  5,5 • 911 = 4,5 см  

Відповідь: OK = 3,5 см; LM = 4,5 см. 

 

Завдання 3 Сторони трикутника відносяться як 5:7:8. Знайдіть невідомі сторони подібного йому трикутника з пери­метром 80 см.

І — 5х

ІІ — 7х

ІІІ — 8х

Р — 20 х — 80 см

Розв’язання   

Нехай 5х (см) – перша сторона, 7х (см) – друга сторона, 8х (см) – третя сторона, тоді 5х + 7х + 8х (см) – периметр. Маємо рівняння.

5х + 7х + 8х = 80

20х = 80

х = 80 : 20

х = 4

5х = 5 • 4 = 20 (см) – І сторона.

7х = 7 • 4 = 28 (см) – ІІ сторона.

8х = 8 • 4 = 32 (см) – ІІІ сторона.

Відповідь: 20 см, 28 см, 32 см.  

 

Завдання 4 На стороні АС трикутника ABC вибрано точ­ку L так, що ∠A = ∠LBC, ВС = 9 см, LC = 6 см. Знайдіть довжину відрізка AL.

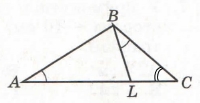
Підказка.

Для трикутника АВС підбираємо слідування відповідних кутів подібного трикутника (від цього залежатиме його назва). 

За умовою ∠A = ∠LBC, кут ∠C – спільний, тоді третя пара відповідних кутів ∠B = ∠BLC). Для ∆АВС подібним стає ∆BLC.  

Розв’язання 

За умовою ∠A = ∠LBC, кут ∠C – спільний, трикутники ∆ABC ~ ∆BLC будуть подібними за двома кутами, якщо відповідні сторони пропорційні.

ABBL = BCLC = ACBC

 

Підставимо числові значення. 

ABBL = 96 = AC9

 

96 = AC9

AC = 9 • 96 = 13,5 (см)

 

AC = AL + LC (основна властивість вимірювання відрізків).

AL = AC – LC = 13,5 см – 6 см = 7,5 см. 

Відповідь: AL = 7,5 см.