ДІАГНОСТИЧНА РОБОТА 2 [4М]

Трапеція. Вписані та описані чотирикутники. Теорема Фалеса. Середні лінії трикутника та трапеції

ВАРІАНТ 1

Завдання 1 Укажіть бічні сторони трапеції KLMF, зображеної на малюнку.

Основи трапеції: KF (або FK), LM(або ML).

Бічні сторони KL (або LK), MF(або FM). 

A KF і LM         Б KF і KL

B LM і MF         Г KL і MF

Завдання 2 Середня лінія рівностороннього трикутника дорівнює 8 см. Знай­діть сторону цього трикутника.

Середня лінія трикутника дорівнює половині паралельної сторони.

8 см • 2 = 16 см

A 4 см        Б 16 см

B 24 см      Г 12 см

Завдання 3 Дано: M₁N₁ || M₂N₂, ОМ₁ = М₁М₂, ON₁ = 4 см. Знайти: ON₂.

За умовою M₁N₁ || M₂N₂, ОМ₁ = М₁М₂, то за теоремою Фалеса ON₁ = N₁N₂.

ON₂ = ON₁ + N₁N₂ = 2ON₁ = 2 • 4 см = 8 см

A 6 см         Б 9 см

B 8 см        Г 7 см

 

Завдання 4 Знайдіть кути М і N чотирикутника MNKL, вписаного в коло, якщо ∠K = 120°, ∠L = 40°.

Для чотирикутника MNKL протилежні кути ∠M і ∠K, ∠N і ∠L.

За умовою чотирикутник вписаний у коло, тому ∠M + ∠K = ∠N + ∠L = 180° (теорема про властивість кутів вписаного чотирикутника).

∠M +∠K = 180°

∠M = 180° – ∠K = 180° – 120° = 60°

∠N + ∠L = 180°

∠N = 180° – ∠L = 180° – 40° = 140°

Відповідь: ∠M = 60°, ∠N = 140°. 

Завдання 5 Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть пери­метр трикутника, сторонами якого є середні лінії цього трикутника.

До кожної сторони трикутника треба провести середню лінію.

Середня лінія трикутника дорівнює половині паралельної сторони.

6 см : 2 = 3 см – довжина І сторони шуканого трикутника. 

8 см : 2 = 4 см – довжина ІІ сторони шуканого трикутника.

10 см : 2 = 5 см – довжина ІІІ сторони шуканого трикутника.

Р = 3 см + 4 см + 5 см = 12 см

Відповідь: 12 см.  

Завдання 6 Середня лінія трапеції дорівнює 10 см. Знайдіть основи трапеції, якщо одна з них на 2 см більша за другу.

Середня лінія трапеція дорівнює половині суми довжин її основ.

Перша основа — х

Інша основа — х + 2

Сер. лінія — 10 см

Розв’язання

Нехай х (см) – перша основа, х + 2 (см) – інша основа, х + (х + 2)2 (см) – середня лінія трапеції. Маємо рівняння.

х + (х + 2)2 = 10

х + х + 2 = 10 • 2

2х + 2 = 20

2х = 20 – 2

2х = 18

х = 18 : 2

х = 9 (см) – перша основа трапеції.

х + 2 = 9 + 2 = 11 (см) – інша основа трапеції.

Відповідь: 9 см, 11 см. 

Завдання 7 У рівнобічну трапецію, периметр якої 28 см, вписано коло. Знайдіть бічну сторону трапеції.

І б. — х

ІІ б. — х

Р2 — 282 см

Бічні сторони рівнобічної трапеції є протилежними, вони рівні. 

За умовою у трапецію вписане коло, то сума протилежних сторін дорівнює півпериметру трапеції (наслідок з теореми про вписаний в коло чотирикутник).

Нехай х (см) – бічна сторона трапеції, 2х (см) – півпериметр. Маємо рівняння.

2х = 28 : 2

2х = 14

х = 14 : 2

х = 7 (см) – бічна сторона рівнобічної трапеції.

Відповідь: 7 см

Завдання 8 У прямокутній трапеції тупий кут дорівнює 120°, а більша бічна сторона і більша основа дорівнюють по 16 см. Знайдіть меншу ос­нову трапеції.

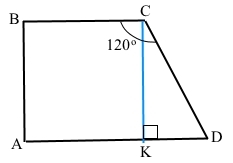
Дано трапеція ABCD – прямокутна, ∠А = ∠В = 90°, ∠С = 120°, СD = АD = 16 см.

∠D = 360° – (90° + 90° + 120°) = 60° (теорема про суму кутів чотирикутника).  

Проведемо з вершини С висоту СК до основи АD, ∆КСD – прямокутний, ВС = АК.

∠КСD = 90° – 60° = 30° (теорема про суму кутів прямокутного трикутника).

КD = 12 СD = 162 = 8 (см) (катет проти кута 30°).

АD = АК + КD = ВС + КD,

звідки ВС = АD – КD = 16 – 8 = 8 (см)

Відповідь: 8 см.

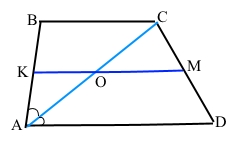
Завдання 9 Діагональ рівнобічної трапеції ділить її тупий кут навпіл, а серед­ню лінію – на відрізки 4 см і 5 см. Знайдіть периметр трапеції.

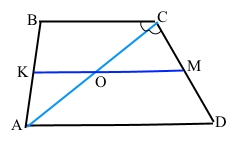
За умовою АВСD – трапеція (ВС || AD), КО = 4 см, ОМ = 5 см; КM – середня лінія трапеції (КМ || AD, КМ || ВС, АК = КВ, СМ = МD), то АО = ОС (теорема  Фалеса). 

КО – середня лінія ∆АВС, ВС = 2КО = 2 • 4 = 8 (см) (за теоремою про середню лінію трикутника).

Аналогічно ОМ – середня лінія ∆АСD, AD = 2ОM = 2 • 5 = 10 (см) (за теоремою про середню лінію трикутника).  

Оскільки діагональ АС лежить на січній до відрізків AD || BC, то внутрішні різносторонні кути рівні ∠ВСА = ∠САD, ∠DCA = ∠BAC, за умовою діагональ АС ділить тупий кут С навпіл (∠ВСА = ∠DСА), звідси ∠САD = ∠ВАС = ∠ВСА = ∠DСА.

∆АВС – рівнобедрений (ознака за рівними кутами при основі), АВ = ВС = 8 см.

∆АСD – рівнобедрений (ознака за рівними кутами при основі), СD = АD = 10 см.

Р = АВ + ВС + СD + АD = 8 + 8 + 10 + 10 = 36 (см).

Відповідь: 36 см. 

 

ВАРІАНТ 2

Завдання 1 Укажіть основи трапеції DEFN на малюнку.

Основи трапеції: DN (або ND), EF (або FE).

Бічні сторони DE (або ED), FN (або NF). 

A DN і DE       Б DN і EF

B DE і FN        Г EF і FN

Завдання 2 Сторона рівностороннього трикутника дорівнює 12 см. Знайдіть се­редню лінію цього трикутника.

У рівностороннього трикутника всі сторони рівні.

Середня лінія трикутника дорівнює половині паралельної сторони.

12 см : 2 = 6 см

A З см          Б 24 см

B 4 см          Г 6 см

Завдання 3 Дано: К₁Р₁ || К₂Р₂, ОР₁ = Р₁Р₂, К₁К₂ = 5 см. Знайти: ОК₂.

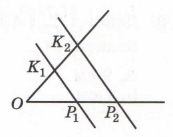
За умовою K₁P₁ || K₂P₂, ОP₁ = P₁P₂, то за теоремою Фалеса OK₁ = K₁K₂.

OK₂ = OK₁ + K₁K₂ = 2K₁K₂ = 2 • 5 см = 10 см

A 10 см        Б 12 см

B 9 см          Г 15 см

Завдання 4  Знайдіть кути А і В чотирикутника ABCD, вписаного в коло, якщо ∠C = 70°, ∠D = 110°.

Для чотирикутника ABCD протилежні кути ∠A і ∠C, ∠B і ∠D.

За умовою чотирикутник вписаний у коло, тому ∠A + ∠C = ∠B + ∠D = 180° (теорема про властивість кутів вписаного чотирикутника).

∠A +∠C = 180°

∠A = 180° – ∠C = 180° – 70° = 110°

∠B + ∠D = 180°

∠B = 180° – ∠D = 180° – 110° = 70°

Відповідь: ∠A = 100°, ∠B = 70°.

Завдання 5 Знайдіть периметр трикутника, якщо його середні лінії дорівню­ють 5 см, 7 см і 8 см.

До кожної сторони трикутника можна провести середню лінію.

Середня лінія трикутника дорівнює половині його паралельної сторони.

5 см • 2 = 10 см – довжина І сторони трикутника.   

7 см • 2 = 14 см – довжина ІІ сторони трикутника.

8 см • 2 = 16 см – довжина ІІІ сторони трикутника.

Р = 10 см + 14 см + 16 см = 40 см

ІІ спосіб

Знайдемо периметр трикутника, утвореного середніми лініями. 

Р = 5 + 7 + 8 = 20 (см)

Середня лінія трикутника дорівнює половині паралельної сторони, то кожна сторона трикутника удвічі більша за паралельну середню лінію, звідси периметр трикутника буде удвічі більшим.

Р • 2 = 20 • 2 = 40 (см) 

Відповідь: 40 см.  

Завдання 6 Середня лінія трапеції дорівнює 12 см. Знайдіть основи трапеції, якщо одна з них на 4 см менша від другої.

Середня лінія трапеція дорівнює половині суми довжин її основ.

Перша основа — х

Інша основа — х – 4

Сер. лінія — 12 см

Розв’язання

Нехай х (см) – перша основа, х – 4 (см) – інша основа, х + (х – 4)2 (см) – середня лінія трапеції. Маємо рівняння.

х + (х – 4)2 = 12

х + х – 4 = 12 • 2

2х – 4 = 24

2х = 24 + 4

2х = 28

х = 28 : 2

х = 14 (см) – перша основа трапеції.

х – 4 = 14 – 4 = 10 (см) – інша основа трапеції.

Відповідь: 14 см, 10 см. 

Завдання 7 Коло вписане в рівнобічну трапецію. Знайдіть периметр трапеції, якщо її бічна сторона дорівнює 5 см.

І б. — 5

ІІ б. — 5

Всього — Р2 см

Бічні сторони рівнобічної трапеції є протилежними, вони рівні. 

За умовою у трапецію вписане коло, то сума протилежних сторін дорівнює півпериметру трапеції (наслідок з теореми про вписаний в коло чотирикутник).

Р2 = 5 + 5

Р2 = 10

Р = 10 • 2

Р = 20 (см) – периметр рівнобічної трапеції.

Відповідь: 20 см.

Завдання 8 У прямокутній трапеції гострий кут дорівнює 60°, а більша основа і більша бічна сторона дорівнюють по 18 см. Знайдіть меншу осно­ву трапеції.

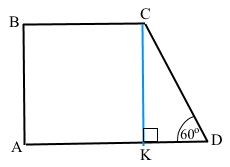
Дано трапеція ABCD – прямокутна, ∠А = ∠В = 90°, ∠D = 60°, СD = АD = 18 см.

Проведемо з вершини С висоту СК до основи АD, ∆КСD – прямокутний, ВС = АК.

∠КСD = 90° – 60° = 30° (теорема про суму кутів прямокутного трикутника).

КD = 1/2 СD = 18/2 = 9 (см) (катет напроти кута 30°).

АD = АК + КD = ВС + КD,

звідки ВС = АD – КD = 18 – 9 = 9 (см)

Відповідь: 9 см.

Завдання 9 Діагональ рівнобічної трапеції ділить її гострий кут навпіл, а се­редню лінію – на відрізки 3 см і 4 см. Знайдіть периметр трапеції.

За умовою АВСD – трапеція (ВС || AD), КО = 3 см, ОМ = 4 см; відрізок КM – середня лінія трапеції (КМ || AD, КМ || ВС, АК = КВ, СМ = МD), то АО = ОС (теорема Фалеса).

Відрізок КО – середня лінія ∆АВС, ВС = 2КО = 2 • 3 = 6 (см) (за теоремою про середню лінію трикутника).

Аналогічно відрізок ОМ – середня лінія ∆АСD, AD = 2ОM = 2 • 4 = 8 (см) (за теоремою про середню лінію трикутника). 

Оскільки діагональ АС лежить на січній до відрізків AD || BC, то внутрішні різносторонні кути рівні ∠ВСА = ∠САD, ∠DCA = ∠BAC, за умовою діагональ АС ділить гострий кут А навпіл (∠CAD = ∠BAC), звідси ∠BCA = ∠DCA = ∠CAD = ∠BAC.

∆АВС – рівнобедрений (ознака за рівними кутами при основі), АВ = ВС = 6 см.

∆АСD – рівнобедрений (ознака за рівними кутами при основі), СD = АD = 8 см.

Р = АВ + ВС + СD + АD = 6 + 6 + 8 + 8 = 28 (см).

Відповідь: 28 см. 

 

ВАРІАНТ 3

Завдання 1 Укажіть основи трапеції CFKL на малюнку.

Основи трапеції: CL (або LC), FK (або KF).

Бічні сторони CF (або FC), KL (або LK). 

A CL і CF         Б FK і KL

B CL і FK        Г CF і KL 

Завдання 2 Середня лінія рівностороннього трикутника дорівнює 6 см. Знай­діть сторону цього трикутника.

У рівностороннього трикутника всі сторони рівні.

Середня лінія трикутника дорівнює половині паралельної сторони.

6 см • 2 = 12 см

A 12 см        Б 18 см

B З см           Г 9 см

Завдання 3 Дано: А₁С₁ || А₂С₂, РА₁ = А₁А₂, РС₁ = 3 см. Знайти: РС₂.

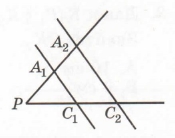
За умовою A₁C₁ || A₂C₂, PA₁ = A₁A₂, то за теоремою Фалеса PC₁ = C₁C₂.

PC₂ = PC₁ + C₁C₂ = 2PC₁ = 2 • 3 см = 6 см

A 9 см        Б 6 см

B 7 см        Г 5 см

Завдання 4  Знайдіть кути Р і L чотирикутника MNPL, вписаного в коло, якщо ∠M = 140°, ∠N = 30°.

Для чотирикутника MNPL протилежні кути ∠M і ∠P, ∠N і ∠L.

За умовою чотирикутник вписаний у коло, тому ∠M + ∠P = ∠N + ∠L = 180° (теорема про властивість кутів вписаного чотирикутника).

∠M +∠P = 180°

∠P = 180° – ∠M = 180° – 140° = 40°

∠N + ∠L = 180°

∠L = 180° – ∠N = 180° – 30° = 150°

Відповідь: ∠P = 40°, ∠L = 150°.

Завдання 5 Сторони трикутника дорівнюють 8 см, 12 см і 14 см. Знайдіть пе­риметр трикутника, сторонами якого є середні лінії цього трикут­ника.

До кожної сторони трикутника треба провести середню лінію.

Середня лінія трикутника дорівнює половині паралельної сторони.

8 см : 2 = 4 см – довжина І сторони шуканого трикутника. 

12 см : 2 = 6 см – довжина ІІ сторони шуканого трикутника.

14 см : 2 = 7 см – довжина ІІІ сторони шуканого трикутника.

Р = 4 см + 6 см + 7 см = 17 см

ІІ спосіб

Знайдемо периметр даного трикутника. 

Р = 8 + 12 + 14 = 34 (см)

Середня лінія трикутника дорівнює половині паралельної сторони, то периметр шуканого трикутника, сторонами якого є середні лінії, буде половина периметра трикутника. 

Р2 = 342 = 17 (см) 

Відповідь: 17 см.   

Завдання 6 Середня лінія трапеції дорівнює 6 см. Знайдіть основи трапеції, якщо одна з них на 2 см менша від другої.

Середня лінія трапеція дорівнює половині суми довжин її основ.

Перша основа — х

Інша основа — х – 2

Сер. лінія — 6 см

Розв’язання

Нехай х (см) – перша основа, х – 2 (см) – інша основа, х + (х – 2)2 (см) – середня лінія трапеції. Маємо рівняння.

х + (х – 2)2 = 6

х + х – 2 = 6 • 2

2х – 2 = 12

2х = 12 + 2

2х = 14

х = 14 : 2

х = 7 (см) – перша основа трапеції.

х – 2 = 7 – 2 = 5 (см) – інша основа трапеції.

Відповідь: 7 см, 5 см. 

Завдання 7 Коло вписане в рівнобічну трапецію, периметр якої 24 см. Знай­діть бічну сторону трапеції.

І б. — х

ІІ б. — х

Р2 — 242 см

Бічні сторони рівнобічної трапеції є протилежними, вони рівні.

За умовою у трапецію вписане коло, то сума протилежних сторін дорівнює півпериметру трапеції (наслідок з теореми про вписаний в коло чотирикутник).

Нехай х (см) – бічна сторона трапеції, 2х (см) – півпериметр. Маємо рівняння.

2х = 24 : 2

2х = 12

х = 12 : 2

х = 6 (см) – бічна сторона рівнобічної трапеції.

Відповідь: 6 см

Завдання 8 У прямокутній трапеції тупий кут дорівнює 120°, більша бічна сто­рона – 10 см, а більша основа – 8 см. Знайдіть меншу основу тра­пеції.

Дано трапеція ABCD – прямокутна, ∠А = ∠В = 90°, ∠С = 120°, СD = 10 см, AD = 8 см.

∠D = 360° – (90° + 90° + 120°) = 60° (теорема про суму кутів чотирикутника).

Проведемо з вершини С висоту СК до основи АD, ∆КСD – прямокутний, ВС = АК.

∠КСD = 90° – 60° = 30° (теорема про суму кутів прямокутного трикутника).

КD = 12 СD = 102 = 5 (см) (катет напроти кута 30°).

АD = АК + КD = ВС + КD,

звідки ВС = АD – КD = 8 – 5 = 3 (см)

Відповідь: 3 см.

Завдання 9 Діагональ рівнобічної трапеції ділить її тупий кут навпіл. Менша основа трапеції дорівнює 10 см, а бічна сторона – 16 см. Визначте довжини відрізків, на які діагональ ділить середню лінію трапеції.

За умовою АВСD – трапеція (ВС || AD), ВС = 10 см,  КM – середня лінія трапеції (КМ || AD, КМ || ВС, АК = КВ, СМ = МD), то АО = ОС (теорема Фалеса).

Відрізок КО – середня лінія ∆АВС, КО = ВС2 = 10 : 2 = 5 (см) (за теоремою про середню лінію трикутника).

Оскільки діагональ АС лежить на січній до відрізків AD || BC, то внутрішні різносторонні кути рівні ∠ВСА = ∠САD, ∠DCA = ∠BAC, за умовою діагональ АС ділить тупий кут С навпіл (∠ВСА = ∠DСА), звідси ∠САD = ∠ВАС = ∠ВСА = ∠DСА.

∆АВС – рівнобедрений (ознака за рівними кутами при основі), ВА = ВС = 10 см, тому СD = 16 см.

∆АСD – рівнобедрений (ознака за рівними кутами при основі), СD = АD = 16 см.

Аналогічно ОМ – середня лінія ∆АСD, ОМ = AD2 = 162 = 8 (см) (за теоремою про середню лінію трикутника). 

Відповідь: 5 см, 8 см. 

ВАРІАНТ 4

Завдання 1  Укажіть бічні сторони трапеції NTKL на малюнку.

Основи трапеції: NK (або KN), TK (або KT).

Бічні сторони NT (або TN), KL (або LK). 

A NT і KL     Б NT і ТК

B KL і NL      Г NL і ТК

Завдання 2 Сторона рівностороннього трикутника дорівнює 18 см. Знайдіть середню лінію цього трикутника.

У рівностороннього трикутника всі сторони рівні.

Середня лінія трикутника дорівнює половині паралельної сторони.

18 см : 2 = 9 см

A 36 см         Б 6 см

B 9 см           Г З см

Завдання 3 Дано: M₁D₁ || M₂D₂, РМ₁ = M₁M₂, D₁D₂ = 6 см. Знайти: PD₂.

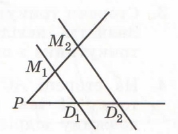
За умовою M₁D₁ || M₂D₂, PM₁ = M₁M₂, то за теоремою Фалеса PD₁ = D₁D₂.

PD₂ = PD₁ + D₁D₂ = 2D₁D₂ = 2 • 6 см = 12 см

A 14 см         Б 10 см

B 8 см           Г 12 см

Завдання 4 Знайдіть кути М і N чотирикутника KLMN, вписаного в коло, якщо ∠K = 130°, ∠L = 60°.

Для чотирикутника KLMN протилежні кути ∠K і ∠M, ∠L і ∠N.

За умовою чотирикутник вписаний у коло, тому ∠K + ∠M = ∠L + ∠N = 180° (теорема про властивість кутів вписаного чотирикутника).

∠K + ∠M = 180°

∠M = 180° – ∠K = 180° – 130° = 50°

∠L + ∠N = 180°

∠N = 180° – ∠L = 180° – 60° = 120°

Відповідь: ∠M = 50°, ∠N = 120°.

Завдання 5 Знайдіть периметр трикутника, якщо його середні лінії дорівню­ють 4 см, 5 см і 6 см.

До кожної сторони трикутника можна провести середню лінію.

Середня лінія трикутника дорівнює половині його паралельної сторони.

4 см • 2 = 8 см – довжина І сторони трикутника.   

5 см • 2 = 10 см – довжина ІІ сторони трикутника.

6 см • 2 = 12 см – довжина ІІІ сторони трикутника.

Р = 8 см + 10 см + 12 см = 30 см

ІІ спосіб

Відповідь: 30 см.  

Завдання 6 Середня лінія трапеції дорівнює 8 см. Знайдіть основи трапеції, якщо одна з них на 4 см більша за другу.

Середня лінія трапеція дорівнює половині суми довжин її основ.

Перша основа — х

Інша основа — х + 4

Сер. лінія — 8 см

Розв’язання

Нехай х (см) – перша основа, х + 4 (см) – інша основа, х + (х + 4) 2 (см) – середня лінія трапеції. Маємо рівняння.

х + (х + 4)2 = 8

 

х + х + 4 = 8 • 2

2х + 4 = 16

2х = 16 – 4

2х = 12

х = 12 : 2

х = 6 (см) – перша основа трапеції.

х + 4 = 6 + 4 = 10 (см) – інша основа трапеції.

Відповідь: 6 см, 10 см. 

Завдання 7 Коло вписане в рівнобічну трапецію. Знайдіть периметр трапеції, якщо її бічна сторона дорівнює 7 см.

І б. — 7

ІІ б. — 7

Всього — Р2 см

Бічні сторони рівнобічної трапеції є протилежними, вони рівні. 

За умовою у трапецію вписане коло, то сума протилежних сторін дорівнює півпериметру трапеції (наслідок з теореми про вписаний в коло чотирикутник).

Р2 = 7 + 7

Р2 = 14

Р = 14 • 2

Р = 28 (см) – периметр рівнобічної трапеції.

Відповідь: 28 см.

Завдання 8 У прямокутній трапеції гострий кут дорівнює 60°, а більша осно­ва – 10 см, більша бічна сторона – 8 см. Знайдіть меншу основу трапеції.

Дано трапеція ABCD – прямокутна, ∠А = ∠В = 90°, ∠D = 60°, АD =10 см, СD = 8 см.

Проведемо з вершини С висоту СК до основи АD, ∆КСD – прямокутний, ВС = АК.

∠КСD = 90° – 60° = 30° (теорема про суму кутів прямокутного трикутника).

КD = 12 СD = 82 = 4 (см) (катет напроти кута 30°).

АD = АК + КD = ВС + КD,

звідки ВС = АD – КD = 10 – 4 = 6 (см)

Відповідь: 6 см.

Завдання 9 Діагональ рівнобічної трапеції ділить її гострий кут навпіл. Більша основа трапеції дорівнює 14 см, а бічна сторона – 8 см. Визначте довжини відрізків, на які діагональ ділить середню лінію трапеції.

За умовою АВСD – трапеція (ВС || AD), AD = 14 см,  КM – середня лінія трапеції (КМ || AD, КМ || ВС, АК = КВ, СМ = МD), то АО = ОС (теорема Фалеса).

Відрізок ОМ – середня лінія ∆АСD, ОМ = AD2 = 142 = 7 (см) (за теоремою про середню лінію трикутника). 

Оскільки діагональ АС лежить на січній до відрізків AD || BC, то внутрішні різносторонні кути рівні ∠ВСА = ∠САD, ∠DCA = ∠BAC, за умовою діагональ АС ділить гострий кут А навпіл (∠CAD = ∠BAC), звідси ∠BCA = ∠DCA = ∠CAD = ∠BAC.

∆АСD – рівнобедрений (ознака за рівними кутами при основі), СD = АD = 14 см, то за умовою ВА = 8 см.

∆АВС – рівнобедрений (ознака за рівними кутами при основі), ВС = ВА = 8 см.

Відрізок КО – середня лінія ∆АВС, КО = BC2 = 8 : 2 = 4 (см) (за теоремою про середню лінію трикутника).

Відповідь: 4 см, 8 см.