САМОСТІЙНА РОБОТА 4 [8М]

Теорема Фалеса. Середні лінії трикутника і трапеції

ВАРІАНТ 1

Завдання 1 Основи трапеції дорівнюють 6 см і 16 см. Укажіть довжину серед­ньої лінії трапеції.

Середня лінія трапеції дорівнює півсумі довжин її основ.

(6 + 16) : 2 = 22 : 2 = 11 (см)

А 8 см       Б 10 см      В 11 см        Г З см

Завдання 2 Відрізок, що сполучає середини бічних сторін рівнобедреного три­кутника, дорівнює 7 см. Знайдіть основу трикутника.

Відрізок, що сполучає середини бічних сторін рівнобедреного три­кутника, буде середньою лінією трикутника. Довжина середньої лінії такого рівнобедреного трикутника дорівнює половині його основи.

За теоремою про властивість середньої лінії трикутника: 

7 • 2 = 14 (см) – основа трикутника.  

Відповідь: 14 сантиметрів.

Завдання 3 На малюнку А₁А₂ = А₂А₃, А₁В₁ || А₂В₂ || А₃В₃, А₁А₂ : В₁В₂ = 5:6,  В₂В₃ – А₂А₃ = 7 см. Знайдіть довжину відрізка B₁B₃.

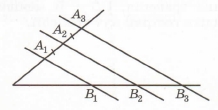
За умовою В₂В₃ – А₂А₃ = 7 см, А₁А₂ = А₂А₃. За теоремою Фалеса В₁В₂ = В₂В₃, звідси В₂В₃ – А₂А₃ = В₁В₂ – А₁А₂ = 7 см.

Нехай х (см) – довжина частини, 5х (см) – довжина А₁А₂, 6х (см) – довжина В₁В₂. Маємо рівняння.

6х – 5х = 7

х = 7

6х = 6 • 7 = 42 (см) – довжина відрізка В₁В₂.

В₁В₃ = В₁В₂ + В₂В₃ (основна властивість вимірювання відрізків), 

В₁В₃ = 2В₁В₂ = 42 • 2 = 84 (см)

Відповідь: В₁В₃ = 84 см.

Завдання 4 Діагоналі трапеції ділять її середню лінію на три частини. Знайдіть довжини цих частин, якщо основи трапеції дорівнюють 8 см і 10 см.

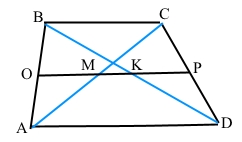
За умовою ОР – середня лінія трапеції, ОР||АD, ОР||ВС, РС = РD і ОВ = ОА.

ОР = (АD + ВС) : 2 = (8 + 10) : 2 = 9 (см) (властивість середньої лінії трапеції).

У ∆ВСDвідрізки ВК = КD (теорема Фалеса), КР – середня лінія трикутника, тому КР = ВС : 2 = 8 см : 2 = 4 см (властивість середньої лінії трикутника).

Аналогічно у ∆АВС, відрізки АМ = МС (за теоремою Фалеса), ОМ – середня лінія трикутника, тому ОМ = ВС : 2 = 8 см : 2 = 4 см (властивість середньої лінії трикутника).

Відрізки ОР = ОМ + МК + КР (основна властивість вимірювання  відрізків), звідси МК = ОР – (ОМ + КР) = 9 см – (4 см + 4 см) = 1 см.    

Відповідь: 4 см, 1 см, 4 см.

ВАРІАНТ 2

Завдання 1 Основи трапеції дорівнюють 8 см і 18 см. Укажіть довжину серед­ньої лінії трапеції.

Середня лінія трапеції дорівнює півсумі довжин її основ.

(8 + 18) : 2 = 26 : 2 = 13 (см)

А 13 см    Б 4 см        В 9 см        Г 12 см

Завдання 2 Основа рівнобедреного трикутника дорівнює 26 см. Знайдіть дов­жину відрізка, що сполучає середини бічних сторін трикутника.

Відрізок, що сполучає середини бічних сторін рівнобедреного три­кутника, буде середньою лінією трикутника. Довжина середньої лінії такого рівнобедреного трикутника дорівнює половині його основи.

За теоремою про властивість середньої лінії трикутника: 

26 : 2 = 13 (см) – довжина середньої лінії трикутника. 

Відповідь: 13 сантиметрів.

Завдання 3 На малюнку N₁N₂ = N₂N₃, M₁N₁ || M₂N₂ || M₃N₃, N₁N₂ : M₁M₂ = 5:4, N₂N₃ – M₂M₃ = 4 см. Знайдіть довжину відрізка M₁M₃.

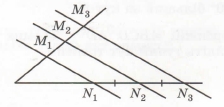
За умовою N₂N₃ – M₂M₃ = 4 см, N₁N₂ = N₂N₃. За теоремою Фалеса M₁M₂ = M₂M₃, звідси N₂N₃ – M₂M₃ = N₁N₂ – M₁M₂ = 4 см.

Нехай х (см) – довжина частини, 5х (см) – довжина N₁N₂, 4х (см) – довжина M₁M₂. Маємо рівняння.

5х – 4х = 4

х = 4

4х = 4 • 4 = 16 (см) – довжина відрізка M₁M₂.

M₁M₃ = M₁M₂ + M₂M₃ (основна властивість вимірювання відрізків), 

M₁M₃ = 2M₁M₂ = 16 • 2 = 32 (см)

Відповідь: M₁M₃ = 32 см.

Завдання 4 Діагоналі трапеції ділять її середню лінію на три частини. Знай­діть довжини цих частин, якщо основи трапеції дорівнюють 10 см і 12 см.

За умовою ОР – середня лінія трапеції, ОР||АD, ОР||ВС, РС = РD і ОВ = ОА.

ОР = (АD + ВС) : 2 = (10 + 12) : 2 = 11 (см) (властивість середньої лінії трапеції).

У ∆ВСD відрізки ВК = КD (теорема Фалеса), КР – середня лінія трикутника, тому КР = ВС : 2 = 10 см : 2 = 5 см (властивість середньої лінії трикутника).

Аналогічно у ∆АВС, відрізки АМ = МС (за теоремою Фалеса), ОМ – середня лінія трикутника, тому ОМ = ВС : 2 = 10 см : 2 = 5 см (властивість середньої лінії трикутника).

Відрізки ОР = ОМ + МК + КР (основна властивість вимірювання  відрізків), звідси МК = ОР – (ОМ + КР) = 12 см – (5 см + 5 см) = 2 см.    

Відповідь: 5 см, 2 см, 5 см.

ВАРІАНТ 3

Завдання 1 Укажіть довжину середньої лінії трапеції, основи якої дорівнюють 4 см і 14 см.

Середня лінія трапеції дорівнює півсумі довжин її основ.

(4 + 14) : 2 = 18 : 2 = 9 (см)

А 10 см    Б 7 см     В 2 см     Г 9 см

Завдання 2 Основа рівнобедреного трикутника дорівнює 16 см. Знайдіть дов­жину відрізка, що сполучає середини бічних сторін трикутника.

Відрізок, що сполучає середини бічних сторін рівнобедреного три­кутника, буде середньою лінією трикутника. Довжина середньої лінії такого рівнобедреного трикутника дорівнює половині його основи.

За теоремою про властивість середньої лінії трикутника: 

16 : 2 = 8 (см) – довжина середньої лінії трикутника.  

Відповідь: 8 сантиметрів.

Завдання 3 На малюнку C₁C₂ = C₂C₃, C₁D₁ || C₂D₂ || C₃D₃, D₁D₂ : C₁C₂ = 7:5, D₂D₃ – C₂C₃ = 6 см. Знайдіть довжину відрізка D₁D₃.

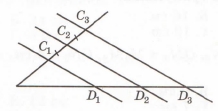
За умовою D₂D₃ – C₂C₃ = 6 см, C₁C₂ = C₂C₃. За теоремою Фалеса D₁D₂ = D₂D₃, звідси D₂D₃ – C₂C₃ = D₁D₂ – C₁C₂ = 6 см.

Нехай х (см) – довжина частини, 7х (см) – довжина D₁D₂, 5х (см) – довжина C₁C₂. Маємо рівняння.

7х – 5х = 6

2х = 6

x = 6 : 2

x = 3

7х = 7 • 3 = 21 (см) – довжина відрізка D₁D₂.

D₁D₃ = D₁D₂ + D₂D₃ (основна властивість вимірювання відрізків), 

D₁D₃ = 2D₁D₂ = 21 • 2 =42 (см)

Відповідь: D₁D₃ = 42 см.

Завдання 4  Діагоналі трапеції ділять її середню лінію на три частини. Знайдіть довжини цих частин, якщо основи трапеції дорівнюють 6 см і 16 см.

За умовою ОР – середня лінія трапеції, ОР||АD, ОР||ВС, РС = РD і ОВ = ОА.

ОР = (АD + ВС) : 2 = (6 + 16) : 2 = 11 (см) (властивість середньої лінії трапеції).

У ∆ВСD відрізки ВК = КD (теорема Фалеса), КР – середня лінія трикутника, тому КР = ВС : 2 = 6 см : 2 = 3 см (властивість середньої лінії трикутника).

Аналогічно у ∆АВС, відрізки АМ = МС (за теоремою Фалеса), ОМ – середня лінія трикутника, тому ОМ = ВС : 2 = 6 см : 2 = 3 см (властивість середньої лінії трикутника).

Відрізки ОР = ОМ + МК + КР (основна властивість вимірювання  відрізків), звідси МК = ОР – (ОМ + КР) = 11 см – (3 см + 3 см) = 5 см   

Відповідь: 3 см, 5 см, 3 см.

ВАРІАНТ 4

Завдання 1 Укажіть довжину середньої лінії трапеції, основи якої дорівнюють 4 см і 18 см.

Середня лінія трапеції дорівнює півсумі довжин її основ.

(4 + 18) : 2 = 22 : 2 = 11 (см)

А 2 см      Б 11 см     В 9 см     Г 10 см

Завдання 2 Відрізок, що сполучає середини бічних сторін рівнобедреного три­кутника, дорівнює 8 см. Знайдіть основу трикутника.

Відрізок, що сполучає середини бічних сторін рівнобедреного три­кутника, буде середньою лінією трикутника. Довжина середньої лінії такого рівнобедреного трикутника дорівнює половині його основи.

За теоремою про властивість середньої лінії трикутника: 

8 • 2 = 16 (см) – основа трикутника

Відповідь: 16 сантиметрів.

Завдання 3 На малюнку K₁K₂ = K₂K₃, A₁K₁ || A₂K₂ || A₃K₃, K₁K₂ : A₁A₂ = 3:2,  K₂K₃ – A₂A₃ = 5 см. Знайдіть довжину відрізка A₁A₃.

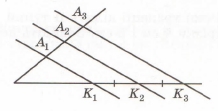
За умовою K₂K₃ – A₂A₃ = 5 см, K₁K₂ = K₂K₃. За теоремою Фалеса A₁A₂ = A₂A₃, звідси K₂K₃ – A₂A₃ = K₁K₂ – A₁A₂ = 5 см.

Нехай х (см) – довжина частини, 3х (см) – довжина K₁K₂, 2х (см) – довжина A₁A₂. Маємо рівняння.

3х – 2х = 5

х = 5

2х = 2 • 5 = 10 (см) – довжина відрізка A₁A₂.

A₁A₃ = A₁A₂ + A₂A₃ (основна властивість вимірювання відрізків), 

A₁A₃ = 2A₁A₂ = 10 • 2 = 20 (см)

Відповідь: A₁A₃ = 20 см.

Завдання 4  Діагоналі трапеції ділять її середню лінію на три частини. Знайдіть довжини цих частин, якщо основи трапеції дорівнюють 4 см і 18 см.

За умовою ОР – середня лінія трапеції, ОР||АD, ОР||ВС, РС = РD і ОВ = ОА.

ОР = (АD + ВС) : 2 = (4 + 18) : 2 = 11 (см) (властивість середньої лінії трапеції).

У ∆ВСD відрізки ВК = КD (теорема Фалеса), КР – середня лінія трикутника, тому КР = ВС : 2 = 4 см : 2 = 2 см (властивість середньої лінії трикутника).

Аналогічно у ∆АВС, відрізки АМ = МС (за теоремою Фалеса), ОМ – середня лінія трикутника, тому ОМ = ВС : 2 = 4 см : 2 = 2 см (властивість середньої лінії трикутника).

Відрізки ОР = ОМ + МК + КР (основна властивість вимірювання  відрізків), звідси МК = ОР – (ОМ + КР) = 11 см – (2 см + 2 см) = 7 см   

Відповідь: 2 см, 7 см, 2 см.