ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Діагностична робота № 2

Паралельні та перпендикулярні прямі

Варіант 1

Завдання 1 На малюнку зображено перпендикулярні прямі.

Прямі можуть бути:

• паралельними,

• перетинатися (у тому числі перпендикулярні прямі).  

А. (паралельні)   Б. (перетинаються)  В. (перпендикулярні)  Г. (перетинаються)

Завдання 2  За малюнком укажіть, як називають кути 1 і 2.

A. внутрішні односторонні

Б. внутрішні різносторонні

B. відповідні 

Г. вертикальні

Завдання 3  На малюнку прямі а і b паралельні, с — січ­на. Знайдіть градусну міру кута х.

Сума внутрішніх односторонніх кутів дорівнює 180°. ∠х = 180° – 85° = 95°

A. 75°                       Б. 85°

B. 95°                       Г. 105°

Завдання 4  На малюнку прямі АВ, CD і MN перетинаються в точці О. Чи є прямі АВ і CD взаємно перпендикулярни­ми, якщо:

1) ∠COM = 72°, ∠MOA = 18°;

∠COA = ∠COM + ∠MOA = 72° + 18° = 90°.

Відповідь: АВ ⊥ CD. 

2) ∠CON = 109°, ∠BON = 20°?

∠CON = ∠COB + ∠BON,

∠COB = ∠CON – ∠BON= 109° – 20° = 89°

∠COB ≠ 90°, тому прямі АВ і CD не є взаємно перпендикулярними.

Відповідь: ні. 

Завдання 5  Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 67°. Знайдіть решту кутів.

При перетині двох паралельних прямих січною утвориться вісім кутів (по 4 однакових кути). Сума внутрішніх односторонніх кутів дорівнює 180, інший внутрішній односторонній кут 180° – 67° = 113°.

Відповідь: 67°, 67°, 67°, 113°, 133°, 113°, 113°. 

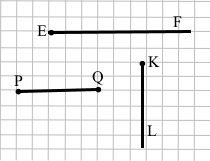
Завдання 6  Накресліть промені EF і KL та відрізок PQ так, щоб про­мінь EF був паралельним відрізку PQ і перпендикулярним до променя KL.

EF || PQ

EF ⊥ KL

Завдання 7  На малюнку прямі АВ, MN і CD перетинаються в точці О, причому АВ ⊥ MN. Знайдіть ∠AOC, якщо ∠MOD = 64°.

Прямі АВ ⊥ MN, тоді ∠MOB = 90°.

За властивістю вимірювання відрізків ∠MOB = ∠MOD + ∠DOB

∠DOB = ∠MOB – ∠MOD = 90°– 64°= 26°

Вертикальні кути ∠AOC = ∠DOB = 26°

Відповідь: ∠AOC = 26°

Завдання 8  За малюнком знайдіть градусну міру кута х.

При січній nвідповідні кути по 80° рівні, тоді а || b.

Вертикальний кут до 70° є внутрішнім одностороннім кутом у парі з ∠х для прямих а || b та січної m,

тоді ∠х = 180° – 70° = 110°.

Відповідь: ∠х = 110°.

Завдання 9  На малюнку АВ || CD. Знайдіть ∠BMC.

Якщо провести уявну пряму с || АВ, а CD ||AB, тоді с || CD.

Для с || АВ та січної ВМ внутрішні різносторонні кути 30°. 

Для с || CD та січної СМ внутрішні різносторонні кути 55°. 

∠BMC = 30° + 55° = 85°

Відповідь: ∠BMC = 85°