ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Самостійна робота № 6

Рівнобедрений трикутник, медіана, бісектриса і висота трикутника, третя ознака рівності трикутників

ВАРІАНТ 1

Завдання 1  На якому з малюнків зображено рівносторонній трикутник?

А рівнобедрений (дві сторони рівні)

Б різносторонній (сторони різні)

В рівносторонній (три сторони рівні)

Г рівнобедрений (дві сторони рівні)

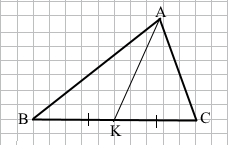
Завдання 2Накресліть гострокутний трикутник ABC. За допомогою лі­нійки з поділками проведіть у ньому медіану АК.

Медіана – відрізок, що сполучає вершину А з точкою К, яка є серединою протилежної сторони ВС.

Завдання 3 Знайдіть сторони рівнобедреного трикутника, якщо його периметр дорівнює 24 см, а основа на 3 см більша за бічну сторону.

У рівнобедреного трикутника бічні сторони рівні.

Нехай х (см) – бічна сторона, х + 3 (см) – основа.

х + х + х + 3 = 24

3х + 3 = 24

3х = 24 – 3

3х = 21

х = 21 : 3

х = 7 (см) – кожна бічна сторона.

х + 3 = 7 + 3 = 10 (см) – основа.

Спосіб ІІ

1) 24 – 3 = 21 (см) – тричі взята бічна сторона.

2) 21 : 3 = 7 (см) – бічна сторона.

3) 7 + 3 = 10 (см) – основа рівнобедреного трикутника.

Відповідь: 7 см , 7 см , 10 см.

Завдання 4 Усередині рівнобедреного трикутника ABC (АВ = АС) узято точку М так, що ВМ = МС. Доведіть, що пряма AM ділить сторону ВС навпіл.

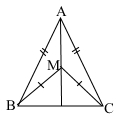
∆АВС – рівнобедрений, АВ = АС, АМ – спільна сторона, ВМ = МС (за умовою), ∆АМВ = ∆АМС (за 3 ознакою рівності трикутників), тоді ∠АМВ = ∠АММ.

Для суміжних кутів ∠АМО = 180 = ∠АМВ + ∠ВМО, ∠АМО = 180 = ∠АМС + ∠СМО, звідси ∠ВМО = ∠СМО. МО – спільна сторона, тоді ∆ВМО = ∆СМО (за 1 ознакою рівності трикутників), ВО = ОС, отже, АМ – пряма, на якій лежить медіана, ділить основу ВС навпіл.