ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Самостійна робота №2

Суміжні та вертикальні кути

Варіант 1

Завдання 1  Прямі AD і ВС перетинаються в точці О. Укажіть пару вертикальних кутів.

A. ∠AOC і ∠AOB                                Б. ∠COD і ∠BOD

B. ∠AOC і ∠BOD                              Г. ∠COD і ∠AOD

Завдання 2  За допомогою транспортира накресліть ∠AKB = 135°. Побу­дуйте суміжний з ним кут за умови, що АК – їхня спільна сторона. Обчисліть градусну міру суміжного кута.

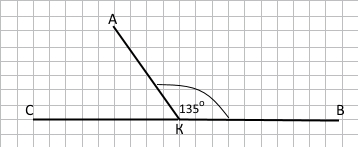
Суміжні кути утворюють розгорнутий кут.

∠СКА + ∠AKB = 180°

∠CKA = 180° – ∠AKB= 180° – 135° = 45°

Відповідь: 45°. 

Завдання 3 Знайдіть градусні міри кожного із чотирьох кутів, що утвори­лися при перетині двох прямих, якщо сума трьох з них дорів­нює 244°.

При перетині двох прямих утворюються дві пари вертикальних кутів, або два суміжні кути. Вертикальні кути рівні.

360° – 244° = 116° – тупий вертикальний кут. 

Різні вертикальні кути є суміжними. 

180° – 116° = 64° – гострий вертикальний кут. 

Відповідь: утворилося чотири кути 116°, 116°, 64°, 64°. 

Завдання 4  Прямі АВ, CD і NM перетинаються в точці О. На малюнку ∠AOC = 25°, ∠MOD = 55°. Знайдіть градусну міру кута NOB.

Три прямі при перетині утворили три пари вертикальних кутів. Вертикальні кути рівні: ∠АОМ = ∠NOB.

Різні вертикальні кути суміжні: ∠COM + ∠AOM + ∠MOD = 180°

∠NOB = ∠AOM = 180° – ∠COM –  ∠MOD= 180° – 25°– 55°= 100°

Відповідь: ∠NOB = 100°.

Варіант 2

Завдання 1  Прямі MN і KL перетинаються в точці О. Укажіть пару вертикальних кутів.

Вертикальні кути рівні.

A. ∠MOK і ∠KON                Б. ∠MOK і ∠LON

B. ∠MOK і ∠LOM                Г. ∠KON і ∠LON

Завдання 2  За допомогою транспортира накресліть ∠ABC = 115°. Побу­дуйте суміжний з ним кут за умови, що АВ – їхня спільна сторона. Обчисліть градусну міру суміжного кута.

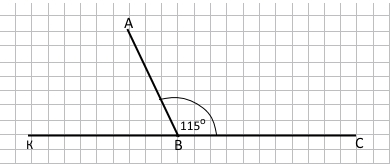
Суміжні кути утворюють розгорнутий кут.

∠KBA + ∠ABC = 180°

∠KBA = 180° – ∠ABC = 180° – 115° = 65°

Відповідь: 65°.

Завдання 3  Знайдіть градусні міри кожного із чотирьох кутів, що утвори­лися при перетині двох прямих, якщо сума трьох з них дорів­нює 216°.

При перетині двох прямих утворюються дві пари вертикальних кутів, або два суміжні кути. Вертикальні кути рівні.

360° – 216° = 114° – тупий вертикальний кут. 

Різні вертикальні кути є суміжними. 

180° – 114° = 66° – гострий вертикальний кут. 

Відповідь: утворилося чотири кути 114°, 114°, 66°, 66°.

Завдання 4  Прямі АВ, CD і KL перетинаються в точці О. На малюнку ∠AOC = 45°, ∠KOB = 75°. Знайдіть градусну міру кута LOD.

Три прямі при перетині утворили три пари вертикальних кутів. Вертикальні кути рівні: ∠LOD = ∠COK.

Різні вертикальні кути суміжні: ∠AOC + ∠COK + ∠KOB = 180°

∠LOD = ∠COK = 180° – ∠AOC – ∠KOD = 180° – 45° – 75° = 60°

Відповідь: ∠LOD = 60°.

Варіант З

Завдання 1  Прямі АВ і CD перетинаються в точці О. Укажіть пару вертикальних кутів.

Вертикальні кути рівні.

A. ∠BOD і ∠AOD                   Б. ∠AOC і ∠AOD

B. ∠AOC і ∠COB                    Г. ∠AOC і ∠BOD

Завдання 2 За допомогою транспортира накресліть ∠CDF = 75°. Побудуй­те суміжний з ним кут за умови, що CD – їхня  спільна сторона. Обчисліть градусну міру суміжного кута.

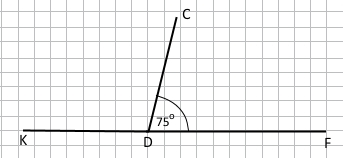
Суміжні кути утворюють розгорнутий кут. 

∠СКА + ∠AKB = 180°

∠CKA = 180° – ∠AKB = 180° – 115° = 65°

Відповідь: 65°.

Завдання 3  Знайдіть градусні міри кожного із чотирьох кутів, що утворилися при перетині двох прямих, якщо сума трьох з них дорівнює 288°.

При перетині двох прямих утворюються дві пари вертикальних кутів, або два суміжні кути. Вертикальні кути рівні.

360° – 288° = 72° – гострий вертикальний кут. 

Різні вертикальні кути є суміжними. 

180° – 72° = 108° – тупий вертикальний кут. 

Відповідь: утворилося чотири кути 108°, 108°, 72°, 72°.

Завдання 4 Прямі АВ, CD і KL перетинаються в точці О. На малюнку ∠AOC = 35°, ∠KOB = 85°. Знайдіть градусну міру кута LOD.

Три прямі при перетині утворили три пари вертикальних кутів. Вертикальні кути рівні: ∠LOD = ∠COK.

Різні вертикальні кути суміжні: ∠AOC + ∠COK + ∠KOB = 180°

∠LOD = ∠COK = 180° – ∠AOC – ∠KOD = 180° – 35° – 85° = 60°

Відповідь: ∠LOD = 60°.

Варіант 4

Завдання 1  Прямі KM і LN перетинаються в точці О. Укажіть пару вертикальних кутів.

Вертикальні кути рівні.

A. ∠KON і ∠NOM                      Б. ∠KON і ∠LOM

B. ∠KOL і ∠LOM                       Г. ∠NOM і ∠LOM

Завдання 2 За допомогою транспортира накресліть ∠MAN = 65°. Побудуйте суміжний з ним кут за умови, що AM – їхня спільна сторона. Обчисліть градусну міру суміжного кута.

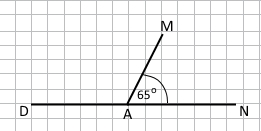
Суміжні кути утворюють розгорнутий кут. 

∠DAM + ∠MAN = 180°

∠DAM = 180° – ∠MAN = 180° – 65° = 115°

Відповідь: 115°.

Завдання 3 Знайдіть градусні міри кожного із чотирьох кутів, що утвори­лися при перетині двох прямих, якщо сума трьох з них дорів­нює 292°.

При перетині двох прямих утворюються дві пари вертикальних кутів, або два суміжні кути. Вертикальні кути рівні.

360° – 292° = 68° – гострий вертикальний кут. 

Різні вертикальні кути є суміжними. 

180° – 68° = 112° – тупий вертикальний кут. 

Відповідь: утворилося чотири кути 112°, 112°, 68°, 68°.

Завдання 4 Прямі АВ, CD і NM перетинаються в точці О. На малюнку ∠AOC = 15°, ∠MOB = 65°. Знай­діть градусну міру кута NOD.

Три прямі при перетині утворили три пари вертикальних кутів. Вертикальні кути рівні: ∠CОМ = ∠NOD.

Різні вертикальні кути суміжні: ∠AOC + ∠COM + ∠MOB = 180°

∠NOD = ∠COM = 180° – ∠AOC – ∠MOB = 180° – 15° – 65° = 100°

Відповідь: ∠NOD = 100°.