ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Самостійна робота №1

Елементарні геометричні фігури та їхні властивості 

Варіант 1

Завдання 1  Пара доповняльних променів.

Мають спільний початок і утворюють кут 180°.

A. OA і ОС                          Б. OA і OD

B. ОВ і OD                          Г. ОВ і ОС

Завдання 2   Накресліть відрізки АВ і CD такі, що АВ = 7 см 2 мм, CD = 6 см 8 мм. Порівняйте довжини відрізків АВ і CD.

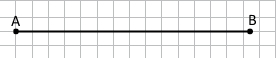
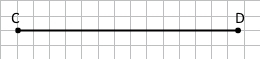
АВ > CD

CD < AB

Завдання 3  Промінь ОМ ділить ﮮAOB на два кути. Знайдіть ﮮAOM, якщо ﮮAOB = 80°, ﮮMOB = 34  ﮮAOB.

∠MOB = 80° : 4 • 3 = 60°

∠AOB = ∠AOM + ∠MOB

∠AOM = ∠AOB – ∠MOB = 80° – 60° = 20°.

Відповідь: ∠AOM = 20°.

Завдання 4 Відрізок MN, довжина якого 16,4 см, поділено на три части­ни. Довжина однієї з них на 2,4 см менша від довжини другої і втричі менша від довжини третьої. Знайдіть довжину мен­шої із цих частин.

Розв’язання

1) 16,4 – 2,4 = 14 (см) – припадає на 5 частин. 

2) 14 : 5 = 2,8 (см) – І відрізок (1 частина)

Відповідь: найменша частина 2,8 см. 

Варіант 2

Завдання 1  Пара доповняльних променів.

Мають спільний початок і утворюють кут 180°.

A. OL і ОМ                        Б. OL і ON

B. ОК і ON                       Г. ОК і ОМ К

Завдання 2  Накресліть відрізки АВ і MN такі, що АВ = 6 см 7 мм, MN = 7 см 3 мм. Порівняйте довжини відрізків АВ і MN.

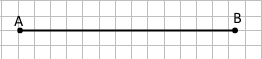
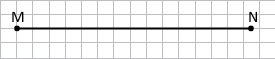
АВ < CD

CD> AB

Завдання 3  Промінь ОК ділить ﮮCOD на два кути. Знайдіть ﮮCOK, якщо ﮮCOD = 100°, ﮮKOD = 45ﮮCOD.

∠KOD = 100° : 5 • 4 = 80°

∠COD = ∠COK + ∠KOD

∠COK = ∠COD – ∠KOD = 100° – 80° = 20°.

Відповідь: ∠COK = 20°.

Завдання 4 Відрізок CD, довжина якого 15,3 см, поділено на три части­ни. Довжина однієї з них удвічі менша від довжини другої і на 2,5 см менша від довжини третьої. Знайдіть довжину меншої із цих частин.

Розв’язання

1) 15,3 – 2,5 = 12,8 (см) – припадає на 4 частини. 

2) 12,8 : 4 = 3,2 (см) – І відрізок (1 частина)

Відповідь: найменша частина 3,2 см. 

Варіант З

Завдання 1  Пара доповняльних променів.

Мають спільний початок і утворюють кут 180°.

A. ОВ і OD                         Б. OD і ОС

B. OA і ОС                         Г. OA і ОВ

Завдання 2  Накресліть відрізки CD і KL такі, що CD = 6 см 4 мм, KL = 5 см 7 мм. Порівняйте довжини відрізків CD і KL.

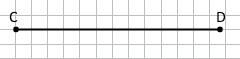
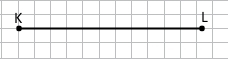
CD > KL

KL < CD

Завдання 3  Промінь OL ділить ﮮCOD на два кути. Знайдіть ﮮCOL, якщо ﮮCOD = 120°, ﮮLOD = 34ﮮCOD.

∠KOD = 120° : 4 • 3 = 90°

∠COD = ∠COL + ∠LOD

∠COL = ∠COD – ∠LOD = 120° – 90° = 30°.

Відповідь: ∠COL = 30°.

Завдання 4 Відрізок АВ, довжина якого 13,8 см, поділено на три частини. Довжина однієї з них утричі менша від довжини другої і на 1,8 см менша від довжини третьої. Знайдіть довжину меншої із цих частин.

Розв’язання

1) 13,8 – 1,8 = 12 (см) – припадає на 5 частин. 

2) 12 : 5 = 2,4 (см) – І відрізок (1 частина)

Відповідь: найменша частина 2,4 см. 

Варіант 4

Завдання 1  Пара доповняльних променів.

Мають спільний початок і утворюють кут 180°.

A. ON і OL                         Б. ON і ОМ

B. ОК і ОМ                       Г. ОК і OL

Завдання 2  Накресліть відрізки АВ і EF такі, що АВ = 5 см 9 мм, EF = 6 см 3 мм. Порівняйте довжини відрізків АВ і EF.

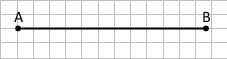
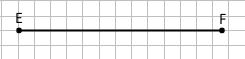
АВ < EF

EF > AB

Завдання 3 Промінь ON ділить ﮮAOB на два кути. Знайдіть ﮮAON, якщо ﮮAOB = 140°, ﮮNOB = 67ﮮAOB.

∠NOB = 140° : 7 • 6 = 120°

∠AOB = ∠AON + ∠NOB

∠AON = ∠AOB – ∠NOB = 140° – 120° = 20°.

Відповідь: ∠AON = 20°.

Завдання 4 Відрізок KL, довжина якого 11,6 см, поділено на три части­ни. Довжина однієї з них на 2,4 см менша від довжини другої і вдвічі менша від довжини третьої. Знайдіть довжину меншої із цих частин.

Розв’язання

1) 11,6 – 2,4 = 9,2 (см) – припадає на 5 частин. 

2) 9,2 : 4 = 2,3 (см) – І відрізок (1 частина)

Відповідь: найменша частина 2,3 см.