
ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)
ГДЗ Геометрія 7 клас
Діагностична робота № 5
Коло і круг
ВАРІАНТ 1
Завдання 1 Знайдіть радіус кола, діаметр якого дорівнює 12 см.
d = 12 см
r = d2 = 12 см : 2 = 6 см
А 12 см Б З см В 6 см Г 24 см
Завдання 2 Знайдіть градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює 80°.
Дуга кола дорівнює центральному куту.
Вписаний кут дорівнює половині відповідної дуги кола.
80° : 2 = 40°
А 80° Б 40° В 160° Г 20°
Завдання 3 На якому з малюнків зображено коло, описане навколо трикутника?
А коло, вписане у трикутник
Б всі вершини трикутника не дотикаються до кола
В всі вершини трикутника не дотикаються до кола
Г коло, описане навколо трикутника (всі вершини трикутника не дотикаються до кола)
Завдання 4 Точка О – центр кола, АВ – його хорда. Знайдіть ∠AOB, якщо ∠OAB = 42°.
Відрізки ОА = ОВ – радіуси кола, ∆АОВ – рівнобедрений, кути при основі ∠OAB = ∠OBA (властивість рівнобедреного трикутника). ∠АОВ = 180° – 2∠ОАВ = 180° – 42°• 2 = 96°.
Відповідь: ∠АОВ = 96°.
Завдання 5 Кола, радіуси яких дорівнюють 7 см і 3 см, мають внутрішній дотик. Знайдіть відстань між центрами цих кіл.
Коло з центром О1 радіуса r1 = 7 см.
Коло з центром О2 радіуса r2 = 3 см.
O1O2 = r1 – r2 = 7 см – 3 см = 4 см
Відповідь: 4 см.
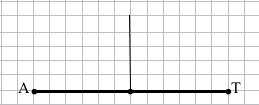
Завдання 6 Накресліть відрізок AT, довжина якого 6 см. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка AT.
6 см : 2 = 3 см
Завдання 7 Два кола мають зовнішній дотик. Відстань між їхніми центрами дорівнює 24 см. Знайдіть радіуси цих кіл, якщо один з них у 5 разів більший за другий.
І радіус — х
ІІ радіус — 5х
Відстань між центрами — 24 см
Нехай х (см) – радіус першого кола, 5х (см) – радіус другого кола.
х + 5х = 24
6х = 24
х = 24 : 6
х = 4 (см) – радіус першого кола.
5х = 4 • 5 = 20 (см) – радіус другого кола.
Відповідь: 4 см, 20 см.
Завдання 8 Побудуйте рівнобедрений трикутник, основа якого дорівнює відрізку а, а кут при основі – куту М (елементи трикутника подано на малюнку).
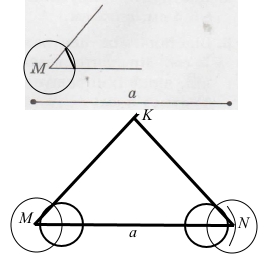
1) На промені відкладаємо відрізок а.
2) Будуємо кут М.
3) Аналогічно будуємо кут N.
4) З’єднуємо кінці відрізка а із точкою перетину променів із початком у точках М і N.
Побудували рівнобедрений трикутник за заданою стороною і кутом при основі.
Завдання 9 Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 4 см і 3 см, починаючи від основи. Знайдіть периметр трикутника.
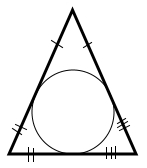
Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
І бічна сторона – 4 см + 3 см
ІІ бічна сторона – 4 см + 3 см
Основа – 4 см + 4 см
(4 + 3) + (4 + 4) + (4 + 3) = 16 + 6 = 22 (см)
Відповідь: 22 см.
ВАРІАНТ 2
Завдання 1 Знайдіть діаметр кола, радіус якого дорівнює 4 см.
r = 4 см
d = 2r = 4 см • 2 = 8 см
А 16 см Б 8 см В 2 см Г 4 см
Завдання 2 Знайдіть градусну міру центрального кута, якщо відповідний йому вписаний кут дорівнює 30°.
Вписаний кут дорівнює половині відповідної дуги кола.
Градусна міра центрального кута дорівнює градусній мірі дуги кола.
30° • 2 = 60°
А 30° Б 90° В 15° Г 60°
Завдання 3 На якому з малюнків зображено коло, описане навколо трикутника?
А всі вершини трикутника не дотикаються до кола
Б коло, описане навколо трикутника (всі вершини трикутника не дотикаються до кола)
В коло, вписане у трикутник
Г всі вершини трикутника не дотикаються до кола
Завдання 4 Точка О – центр кола, MN – його хорда. Знайдіть ∠MNO, якщо ∠MON = 54°.
Відрізки ОM = ОN – радіуси кола, ∆MON – рівнобедрений, кути при основі ∠OMN = ∠ONM (властивість рівнобедреного трикутника). ∠MNO = (180° – ∠MON) : 2 = (180° – 54°) : 2 = 63°.
Відповідь: ∠MNO = 63°.
Завдання 5 Кола, радіуси яких дорівнюють 5 см і 2 см, мають зовнішній дотик. Знайдіть відстань між центрами цих кіл.
Коло з центром О1 радіуса r1 = 5 см.
Коло з центром О2 радіуса r2 = 2 см.
O1O2 = r1 + r2 = 5 см + 2 см = 7 см
Відповідь: 7 см.
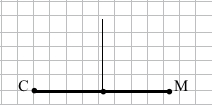
Завдання 6 Накресліть відрізок СМ, довжина якого 42 мм. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка СМ.
42 мм : 2 = 21 мм
Завдання 7 Два кола мають внутрішній дотик. Знайдіть радіуси цих кіл, якщо один з них утричі більший за другий, а відстань між центрами кіл дорівнює 14 см.
І радіус — х
ІІ радіус — 3х
Відстань між центрами — 14 см
Нехай х (см) – радіус першого кола, 3х (см) – радіус другого кола.
3х – х = 14
2х = 14
х = 14 : 2
х = 7 (см) – радіус першого кола.
3х = 7 • 3 = 21 (см) – радіус другого кола.
Відповідь: 7 см, 21 см.
Завдання 8
Побудуйте рівнобедрений трикутник, основа якого дорівнює відрізку b, а кут при основі – куту К (елементи трикутника подано на малюнку).
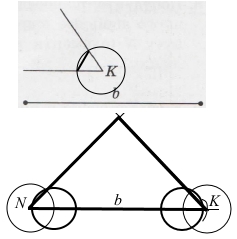
1) На промені відкладаємо відрізок b.
2) Будуємо кут K.
3) Аналогічно будуємо кут N.
4) З’єднуємо кінці відрізка b із точкою перетину променів із початком у точках N і K.
Побудували рівнобедрений трикутник за заданою стороною і кутом при основі.
Завдання 9 Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 3 см і 5 см, рахуючи від вершини, що лежить проти основи. Знайдіть периметр трикутника.

Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
І бічна сторона – 3 см + 5 см
ІІ бічна сторона – 3 см + 5 см
Основа – 5 см + 5 см
(3 + 5) + (5 + 5) + (3 + 5) = 20 + 6 = 26 (см)
Відповідь: 26 см.
ВАРІАНТ З
Завдання 1 Знайдіть радіус кола, діаметр якого дорівнює 16 см.
d = 16 см
r = d2 = 16 см : 2 = 8 см
А 4 см Б 32 см В 16 см Г 8 см
Завдання 2 Знайдіть градусну міру кута, вписаного в коло, якщо відповідний йому центральний кут дорівнює 60°.
Дуга кола дорівнює центральному куту.
Вписаний кут дорівнює половині відповідної дуги кола.
60° : 2 = 30°
А 30° Б 60° В 15° Г 120°
Завдання 3 На якому з малюнків зображено коло, описане навколо трикутника?
А коло, вписане у трикутник
Б всі вершини трикутника не дотикаються до кола
В коло, описане навколо трикутника (всі вершини трикутника не дотикаються до кола)
Г всі вершини трикутника не дотикаються до кола
Завдання 4 Точка О – центр кола, CD – його хорда. Знайдіть ∠OCD, якщо ∠COD = 88°.
Відрізки ОC = ОD – радіуси кола, ∆COD – рівнобедрений, кути при основі ∠OCD = ∠ODC (властивість рівнобедреного трикутника). ∠OCD = (180° – ∠COD) : 2 = (180° – 88°) : 2 = 46°.
Відповідь: ∠OCD = 46°.
Завдання 5 Кола, радіуси яких дорівнюють 8 см і 3 см, мають внутрішній дотик. Знайдіть відстань між центрами цих кіл.
Коло з центром О1 радіуса r1 = 8 см.
Коло з центром О2 радіуса r2 = 3 см.
O1O2 = r1 – r2 = 8 см – 3 см = 5 см
Відповідь: 5 см.
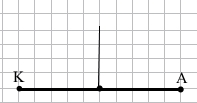
Завдання 6 Накресліть відрізок КА, довжина якого 5 см. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка КА.
5 см : 2 = 2 см 5 мм
Завдання 7 Два кола мають зовнішній дотик. Знайдіть їхні радіуси, якщо один з них у 4 рази більший за другий, а відстань між центрами кіл дорівнює 15 см.
І радіус — х
ІІ радіус — 4х
Відстань між центрами — 15 см
Нехай х (см) – радіус першого кола, 4х (см) – радіус другого кола.
х + 4х = 15
5х = 15
х = 15 : 5
х = 3 (см) – радіус першого кола.
4х = 4 • 3 = 12 (см) – радіус другого кола.
Відповідь: 3 см, 12 см.
Завдання 8 Побудуйте рівнобедрений трикутник, основа якого дорівнює відрізку с, а кут при основі - куту N (елементи трикутника подано на малюнку).
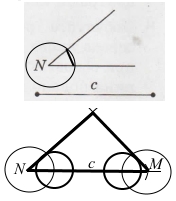
1) На промені відкладаємо відрізок c.
2) Будуємо кут N.
3) Аналогічно будуємо кут M.
4) З’єднуємо кінці відрізка c із точкою перетину променів із початком у точках N і M.
Побудували рівнобедрений трикутник за заданою стороною і кутом при основі.
Завдання 9 Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 2 см і 7 см, починаючи від основи. Знайдіть периметр трикутника.

Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
І бічна сторона – 7 см + 2 см
ІІ бічна сторона – 7 см + 2 см
Основа – 2 см + 2 см
(7 + 2) + (2 + 2) + (7 + 2) = 8 + 14 = 22 (см)
Відповідь: 22 см.
ВАРІАНТ 4
Завдання 1 Знайдіть діаметр кола, радіус якого дорівнює 6 см.
r = 6 см
d = 2r = 6 см • 2 = 12 см
А 24 см Б З см Б 12 см Г 6 см
Завдання 2 Знайдіть градусну міру центрального кута, якщо відповідний йому вписаний кут дорівнює 40°.
Вписаний кут дорівнює половині відповідної дуги кола.
Градусна міра центрального кута дорівнює градусній мірі дуги кола.
40° • 2 = 80°
А 160° Б 40° В 80° Г 20°
Завдання 3 На якому з малюнків зображено колі описане навколо три кутника?
А всі вершини трикутника не дотикаються до кола
Б коло, вписане у трикутник
В всі вершини трикутника не дотикаються до кола
Г коло, описане навколо трикутника (всі вершини трикутника не дотикаються до кола)
Завдання 4 Точка О – центр кола, KL – його хорда. Знайдіть градусну міру кута ∠KOL, якщо ∠OLK = 52°.
Відрізки ОK = ОL – радіуси кола, ∆KOL – рівнобедрений, кути при основі ∠OLK = ∠OKL (властивість рівнобедреного трикутника). ∠KOL = 180° – 2∠ОLK = 180° – 52°• 2 = 76°.
Відповідь: ∠KOL = 76°.
Завдання 5 Кола, радіуси яких дорівнюють 5 см і 3 см, мають зовнішній дотик. Знайдіть відстань між цент рами цих кіл.
Коло з центром О1 радіуса r1 = 5 см.
Коло з центром О2 радіуса r2 = 3 см.
O1O2 = r1 + r2 = 5 см + 3 см = 8 см
Відповідь: 8 см.
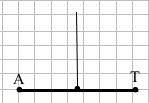
Завдання 6 Накресліть відрізок AT, довжина якого 36 мм. За допомогою лінійки з поділками і косинця проведіть серединний перпендикуляр до відрізка AT.
36 мм : 2 = 18 мм = 1 см 8 мм
Завдання 7 Два кола мають внутрішній дотик. Радіус одного з них у 4 рази більший за радіус другого. Знайдіть радіуси кіл, якщо відстань між їхніми центрами дорівнює 21 см.
І радіус — х
ІІ радіус — 4х
Відстань між центрами — 21 см
Нехай х (см) – радіус першого кола, 4х (см) – радіус другого кола.
4х – х = 21
3х = 21
х = 21 : 3
х = 7 (см) – радіус першого кола.
4х = 7 • 4 = 28 (см) – радіус другого кола.
Відповідь: 7 см, 28 см.
Завдання 8 Побудуйте рівнобедрений трикутник, основа якого дорівнює відрізку а, а кут при основі куту К (елементи трикутника подано на малюнку).
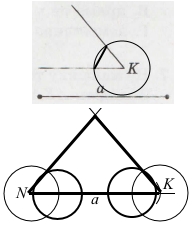
1) На промені відкладаємо відрізок a.
2) Будуємо кут K.
3) Аналогічно будуємо кут N.
4) З’єднуємо кінці відрізка a із точкою перетину променів із початком у точках N і K.
Побудували рівнобедрений трикутник за заданою стороною і кутом при основі.
Завдання 9 Коло, вписане в рівнобедрений трикутник, ділить його бічну сторону на відрізки 7 см і 5 см, починаючи від вершини, що лежить проти основи. Знайдіть периметр трикутника.

Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
І бічна сторона – 7 см + 5 см
ІІ бічна сторона – 7 см + 5 см
Основа – 5 см + 5 см
(7 + 5) + (5 + 5) + (7 + 5) = 20 + 14 = 34 (см)
Відповідь: 34 см.