ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Діагностична робота № 4

Сума кутів трикутника, зовнішній кут трикутника, прямокутні трикутники, нерівність трикутника

ВАРІАНТ 1

Завдання 1  Три кути трикутника можуть дорівнювати...

Сума кутів трикутника дорівнює 180°.

20° + 30° + 40° = 90°, 90° < 180° (не може)

20° + 30° + 120° = 170°, 170° < 180° (не може)

70° + 100° + 10° = 180° (може)

A 20°; 30°; 40°                       Б 70°; 100°; 10°

B 20°; 30°; 120°                     Г 60°; 60°; 70°

 

Завдання 2 У трикутнику ABC АВ < ВС. Порівняйте між собою кути А і С цього трикутника.

Проти меншої сторони трикутника лежить менший кут.

Проти сторони АВ лежить кут С, проти сторони ВС лежить кут А.

Якщо АВ < ВС, тоді  ∠С < ∠А  (∠А > ∠С)

A ∠A < ∠C            Б ∠A = ∠C

B ∠A > ∠C           Г порівняти неможливо

 

Завдання 3  З'ясуйте, за якими елементами прямокутні трикутники, зо­бражені на малюнку, рівні між собою.

На малюнку зображені два прямокутні трикутники.

У них рівні катети, а кут між ними 90° (відповідає першій ознаці рівності трикутників).

A за катетом і гіпотенузою                             Б за катетом і прилеглим гострим кутом

B за катетом і протилежним гострим кутом     Г за двома катетами

 

Завдання 4 Кут при основі рівнобедреного трикутника дорівнює 62°. Знайдіть кут при його вершині.

У рівнобедреного трикутника кути при основі рівні. Сума кутів трикутника дорівнює 180°.

1) 62 + 62 = 124 (°) – сума кутів при основі.

2) 180 – 124 = 56 (°) – кут при вершині рівнобедреного трикутника.

Відповідь: 56°.

 

Завдання 5 На малюнку LH – висота трикутника KLM. ∠КLH = 15°, ∠HLM = 65°. Знайдіть кути цього трикутника.

Розглянемо трикутник KLM.

∠L = ∠KLH + ∠HLM = 15° + 65° = 80° (властивість кутів).

Розглянемо прямокутний трикутник HLM.

∠М = 90° – ∠HLM = 90° – 65° = 25° (сума гострих кутів прямокутного трикутника  дорівнює 90°).

Розглянемо трикутник KLM.

∠К = 180° – (∠L + ∠M) = 180° – (80° + 25°) = 75° (сума кутів трикутника дорівнює 180°)

Відповідь: ∠L = 80°, ∠M = 25°, ∠K = 75°.     

 

Завдання 6 Дві сторони трикутника дорівнюють 4,3 см і 7,2 см. Якому найбільшому цілому числу сантиметрів може дорівнювати третя сторона?

4,3 + 7,2 = 11,6 (см) – сума двох сторін трикутника.

Довжина найбільшої сторони трикутника завжди більша за суму двох інших сторін.

Третя сторона може дорівнювати 12 см.

Відповідь: 12 см.

 

Завдання 7 Один з кутів трикутника утричі менший від другого й на 15° більший за третій. Знайдіть кути трикутника.

Нехай х (°) – перший кут, тоді 3х (°) – другий кут, х – 15 (°) – третій кут трикутника.

Сума кутів трикутника дорівнює 180°.

х + 3х + х – 15 = 180

5х – 15 = 180

5х = 180 + 15

5х = 195

х = 195 : 5

х = (150 + 45) : 5

х = 39 (°) – перший кут.

3х = 39 • 3 = (30 + 9) • 3 = 117 (°) – другий кут.

х – 15 = 39 – 15 = 24 (°) – третій кут.

Відповідь: 39°, 117°, 24°.

 

Завдання 8 Один із зовнішніх кутів трикутника дорівнює 105°. Знайдіть внутрішні кути, не суміжні з ним, якщо вони відносяться як 4 : 3.

Нехай х (°) – частина, тоді 4х (°) – І внутрішній кут, 3х (°) – ІІ внутрішній кут.

Суміжний кут при внутрішньому куті трикутника дорівнює сумі двох інших внутрішніх кутів трикутника.

4х + 3х = 105

7х = 105

х = 105 : 7

х = (70 + 35) : 7

х = 15 (°) – частина.

4х = 15 • 4 = (10 + 5) • 4 = 60 (°) – І внутрішній кут.

3х = 15 • 3 = (10 + 5) • 3 = 45 (°) – ІІ внутрішній кут.

Відповідь: 45°, 60°.

 

Завдання 9 У трикутнику PDM ∠M = 90°, ∠P = 30°, DK – бісектриса три­кутника. Знайдіть довжину катета MP, якщо МК = 5 см.

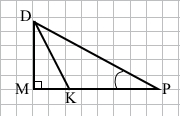
Сума гострих кутів прямокутного трикутника дорівнює 90°.

∠D = 90° – Р = 90° – 30° = 60°

DК – бісектриса кута D, ∠MDK = ∠KDP = ∠D : 2 = 60 : 2 = 30°.  

У прямокутному трикутнику MDKDК катет МК проти кута 30° дорівнює половині гіпотенузи.   

KD = 2MK= 5 см • 2 = 10 см.

Трикутник DKP – рівнобедрений (ознака за двома рівними кутами).

KP = KD = 10 см.

MP = MK + KD = 5 см + 10 см = 15 см

Відповідь: катет МР = 15 см.