ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Самостійна робота № 10

Коло, описане навколо трикутника, центральні та вписані кути, взаємне розміщення двох кіл, основні задачі на побудову

ВАРІАНТ 1

Завдання 1  Малюнок, на якому пряма l є серединним перпенди­куляром до відрізка АВ.

А  l ﬩ АВ, точка перетину не ділить відрізок пополам.

Б  l ﬩ АВ, точка перетину не ділить відрізок пополам.

В пряма l не є перпендикулярною до відрізка АВ.

Г l ﬩ АВ, точка перетину ділить відрізок пополам.

 

Завдання 2  Побудуйте трикутник зі сторонами а = 6 см, b = 4 см, с = 5 см.

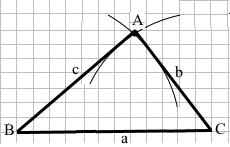
а = ВС = 6 см, b = АС = 4 см, с = АВ = 5 см.

Креслимо відрізок а = ВС = 6 см.

Описуємо дугу кола з центром у точці C радіусом 4 см.

Описуємо дугу кола з центром у точці B радіусом 5 см.

Точка А – точка перетину дуг.

Проводимо відрізки b = AC, c = AB.

 

Завдання 3  Відстань між центрами двох кіл дорівнює 6 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють:

1) 8 см і 2 см:

6 см = 8 см – 2 см 

Кола дотикаються, внутрішній дотик двох кіл.   

2) 5 см і 3 см:

5 см – 3 см < 6 см < 5 см + 3 см

Кола перетинаються.

3) 2 см і 3 см:

6 см > 2 см + 3 см

Кола не перетинаються.

 

Завдання 4 О – центр кола, ∠KDC = 65°. Знайдіть ∠KLD.

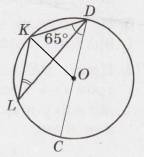
Проведемо відрізок ОК. Радіуси ОК = OD кола  з центром у точці О, ∆DOK – рівнобедрений, ∠DKO = ∠KDO = ∠KDC = 65° (властивість кутів рівнобедреного трикутника).

∠KOD = 180° – 2∠DKO = 180° – 65°• 2 = 50° (сума кутів трикутника).    

◡ KD = 50° (дуга кола центрального кута), ∠KLD =  12 ◡ KD = 50° : 2 = 25° (градусна міра вписаного кута).

Відповідь:  ∠KLD = 25°.

 

ВАРІАНТ 2

Завдання 1 Укажіть малюнок, на якому пряма m є серединним перпенди­куляром до відрізка CD.

А m ﬩ CD, точка перетину не ділить відрізок пополам.

Б   пряма mне є перпендикулярною до відрізка CD

В  m ﬩ CD, точка перетину ділить відрізок пополам.

Г   m ﬩ CD, точка перетину не ділить відрізок пополам.

 

Завдання 2 Побудуйте трикутник зі сторонами a, b і с, якщо а = 5 см, b = 3 см, с = 4 см.

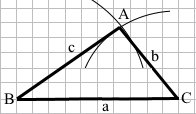
а = ВС = 5 см, b = АС = 3 см, с = АВ = 4 см.

Креслимо відрізок а = ВС = 5 см.

Описуємо дугу кола з центром у точці С радіусом 3 см.

Описуємо дугу кола з центром у точці В радіусом 4 см.

Точка А – точка перетину дуг.

Проводимо відрізки b = AC, c = AB.

 

Завдання 3 Відстань між центрами двох кіл дорівнює 8 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють:

1) 4 см і 7 см:

7 см – 4 см < 8 см < 4 см + 7 см

Кола перетинаються.

2) 5 см і 2 см:

8 см > 2 см + 5 см

Кола не перетинаються.

3) 3 см і 5 см:

8 см = 3 см + 5 см

Кола дотикаються, зовнішній дотик двох кіл.  

 

Завдання 4   О – центр кола, ∠MBA = 35°. Знайдіть ∠NMA.

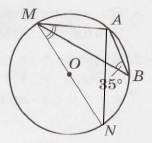
Проведемо відрізок AN. Кут ∠MNA = ∠MBA = 35° (внутрішні кути спираються на одну дугу).

Відрізок MN – радіус кола, звідси ∠MAN = 90° (радіус видно під прямим кутом), ∆MAN – прямокутний.

∠NMA = 90° – ∠MNA= 90° – 35° = 55° (теорема про гострі кути прямокутного трикутника).

Відповідь:  ∠NMA = 55°.

 

ВАРІАНТ З

Завдання 1 Малюнок, на якому пряма l є серединним перпенди­куляром до відрізка CD.

А  пряма l не є перпендикулярною до відрізка CD.

Б   l ﬩ CD, точка перетину ділить відрізок пополам.

В  l ﬩ CD, точка перетину не ділить відрізок пополам.

Г  l ﬩ CD, точка перетину не ділить відрізок пополам.

 

Завдання 2  Побудуйте трикутник зі сторонами а, Ь і с, якщо а = 6 см, b = 3 см, с = 4 см.

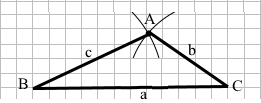
а = ВС = 6 см, b = АС = 3 см, с = АВ = 4 см.

Креслимо відрізок а = ВС = 6 см.

Описуємо дугу кола з центром у точці С радіусом 3 см.

Описуємо дугу кола з центром у точці В радіусом 4 см.

Точка А – точка перетину дуг.

Проводимо відрізки b = AC, c = AB.

 

Завдання 3 Відстань між центрами двох кіл дорівнює 9 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють:

1) 4 см і 3 см:

9 см > 4 см + 3 см

Кола не перетинаються.

2) 4 см і 5 см:

9 см = 4 см  + 5 см

Кола дотикаються, зовнішній дотик двох кіл.  

3) 6 см і 4 см:

6 см – 4 см < 9 см < 6 см + 4 см

Кола перетинаються.

 

Завдання 4 О – центр кола, ∠KLA = 40°. Знайдіть ∠KAB.

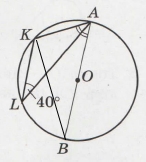
Проведемо відрізок КВ. Кут ∠KВA = ∠KLA = 40° (внутрішні кути спираються на одну дугу).

Відрізок AB – радіус кола, звідси ∠AKB = 90° (радіус видно під прямим кутом), ∆AKB – прямокутний.

∠KAB = 90° – ∠KBA= 90° – 40° = 50° (теорема про гострі кути прямокутного трикутника).

Відповідь:  ∠KAB = 50°.

 

 

ВАРІАНТ 4

Завдання 1 Малюнок, на якому пряма m є серединним перпенди­куляром до відрізка АВ.

А  m ﬩ АВ, точка перетину не ділить відрізок пополам.

Б  m ﬩ АВ, точка перетину не ділить відрізок пополам.

В  пряма mне є перпендикулярною до відрізка АВ.

Г   m ﬩ АВ, точка перетину ділить відрізок пополам.

 

Завдання 2  Побудуйте трикутник зі сторонами a, b і с, якщо а = 5 см, b= 4 см, с = 2 см.

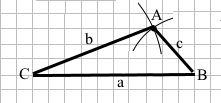
а = ВС = 5 см, b = АС = 4 см, с = АВ = 2 см.

Креслимо відрізок а = ВС = 5 см.

Описуємо дугу кола з центром у точці С радіусом 4 см.

Описуємо дугу кола з центром у точці В радіусом 2 см.

Точка А – точка перетину дуг.

Проводимо відрізки b = AC, c = AB.

 

Завдання 3 Відстань між центрами двох кіл дорівнює 7 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють:

1) 4 см і 5 см;

5 см – 4 см < 7 см < 4 см + 5 см

Кола перетинаються.

2) 4 см і 2 см;

7 см > 4 см + 2 см

Кола не перетинаються.

3) 9 см і 2 см.

7 см = 9 см – 2 см 

Кола дотикаються, внутрішній дотик двох кіл.  

 

Завдання 4 О – центр кола, ∠LKM = 70°. Знайдіть ∠KNM.

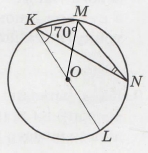
Проведемо відрізок ОM. Радіуси ОК = OM кола  з центром у точці О, ∆KOM – рівнобедрений, ∠OKM = ∠OKM = ∠LKM = 70° (властивість кутів рівнобедреного трикутника).

∠KOM = 180° – 2∠OKM = 180° – 70°• 2 = 40° (сума кутів трикутника).    

◡ KM = 40° (дуга кола центрального кута), ∠KNM =  12 ◡ KM = 40° : 2 = 20° (градусна міра вписаного кута).

Відповідь:  ∠KNM = 20°.