ГДЗ Геометрія 7 клас зошит Самостійні та діагностичні роботи Істер НУШ (відповіді)

Самостійна робота № 9

Коло, круг, дотична до кола, коло, вписане у трикутник

ВАРІАНТ 1

Вправа 1 На малюнку коло, вписане у трикутник.

Коло всередині трикутника дотикається до трьох його сторін.

А (до 2-х сторін)   Б (не дотикається)   В (до 3-х сторін)     Г (до 2-х сторін)

 

Завдання 2 Накресліть коло радіуса 22 мм. Проведіть у ньому діаметр АВ та хорду NM. За допомогою косинця проведіть дотичну до кола, що проходить через точку В.

 

Завдання 3 На малюнку точка О – центр кола, ∠AOK = 38°. Знайдіть ∠OKB.

Сума суміжних кутів 180°.

∠КОВ = 180 – ∠АОК = 180° – 38° = 142°.

ОК = ОВ – радіуси кола. Трикутник КОВ – рівнобедрений.

∠ОКВ = ∠ОВК.

ОКВ = (180° – 142°) : 2 = 38° : 2 = 19°

Відповідь: ∠OKB = 19°.

 

Завдання 4  З точки К, що лежить поза колом, проведено дві дотичні. Відстань від точки К до центра кола дорівнює 14 см. Знайдіть кут між дотичними, якщо радіус кола дорівнює 7 см.

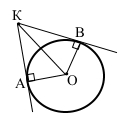
За умовою КО = 14 см, ОВ = 7 см, КА і KB – дотичні,  ∠KAO = ∠KBO = 90°, трикутники KAO і KBO – прямокутні. Оскільки катет дорівнює половині гіпотенузи, то кут навпроти нього ∠ВКО = 30°, відповідно ∠АКО = 30°.  ∠АКВ = ∠АКО + ∠ВКО = 30 + 30 = 60°.

Відповідь: 60°.

 

Вправа 1 На малюнку коло, вписане у трикутник.

Коло, вписане у трикутник, дотикається до трьох його сторін.

А (до 2-х сторін)   Б (до жодної)   В (до 3-х сторін)     Г (до 2-х сторін)

 

Завдання 2 Накресліть коло радіуса 22 мм. Проведіть у ньому діаметр АВ та хорду NM. За допомогою косинця проведіть дотичну до кола, що проходить через точку В.

 

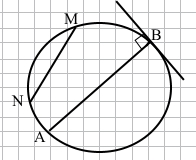
Завдання 3 На малюнку точка О – центр кола, ∠AOK = 38°. Знайдіть ∠OKB.

Сума суміжних кутів 180°.

∠КОВ = 180° – ∠АОК = 180° – 38° = 142°.

ОК = ОВ – радіуси кола. Трикутник КОВ – рівнобедрений.

∠ОКВ = ∠ОВК.

∠ОКВ = (180° – ∠АОК) =  (180° – 142°) : 2 = 38° : 2 = 19°

Відповідь: ∠OKB = 19°.

 

Завдання 4  З точки К, що лежить поза колом, проведено дві дотичні. Відстань від точки К до центра кола дорівнює 14 см. Знайдіть кут між дотичними, якщо радіус кола дорівнює 7 см.

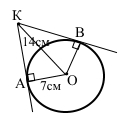
За умовою КО = 14 см, ОВ = 7 см, КА і KB – дотичні,  ∠KAO = ∠KBO = 90°, катети OA = OB – радіуси кола, гіпотенуза ОК – спільна, прямокутні трикутники  ∆KAO = ∆KBO (за катетом і гіпотенузою). Оскільки катет дорівнює половині гіпотенузи, то кут навпроти нього ∠ВКО = 30°, відповідно ∠АКО = 30°.  ∠АКВ = ∠АКО + ∠ВКО = 30° + 30° = 60°.

Відповідь: 60°.

 

 

ВАРІАНТ 2

Завдання 1 На малюнку зображено коло, вписане у трикутник.

Коло, вписане у трикутник, дотикається до трьох його сторін.

А (до 2-х сторін)         Б (до жодної)      В (до жодної)    Г (до 3-х сторін)

 

Завдання 2 Накресліть коло радіуса 23 мм. Проведіть у ньому діаметр CD та хорду PL. Проведіть за допомогою косинця дотичну до кола, що проходить через точку С.

 

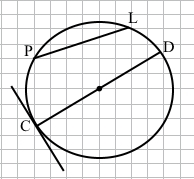
Завдання 3 На малюнку точка О – центр кола, ∠CAO = 28°. Знайдіть ∠AOD.

ОС = ОА – радіуси кола. Трикутник СОА – рівнобедрений.

∠АСО = ∠САО.

∠СОА = 180° – 2∠САО = 180° – 28° • 2 = 124°

Сума суміжних кутів 180°.

∠AOD = 180° – ∠CОA = 180° – 124° = 56°.

Відповідь: ∠AOD = 56°.

 

Завдання 4 Прямі АВ і АС дотикаються до кола із центром О в точках В і С, ∠BAC = 60°, AO = 12 см. Знай­діть радіус кола.

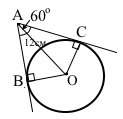
За умовою АВ і АС – дотичні,  ∠АВО = ∠АСО = 90°. Катети ОВ = ОС – радіуси кола, гіпотенуза АО – спільна сторона, ∆АВО = ∆АСО (за катетом і гіпотенузою). Відповідні кути ∠ВАО = ∠САО, ∠ВАС = ∠ВАО + ∠САО = 60°, ∠ВАО = 1/2 ∠ВАС = 1/2 • 60° = 30°. Звідси ОВ = 1/2 АО = 1/2 • 12 см = 6 см (катет проти кута 30° дорівнює половині гіпотенузи).

Відповідь: 6 см.

 

 

ВАРІАНТ З

Завдання 1 На малюнку зображено коло, вписане у трикутник.

Коло, вписане у трикутник, дотикається до трьох його сторін.

А (до жодної)       Б (до трьох)   В (до 2-х сторін)    Г (до жодної)

 

Завдання 2 Накресліть коло радіуса 24 мм. Проведіть у ньому діаметр MN та хорду АК. За допомогою косинця проведіть дотичну до кола, що проходить через точку М.

 

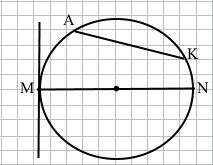
Завдання 3 На малюнку точка О – центр кола, ∠AOL = 78°. Знайдіть ∠AKL.

Сума суміжних кутів 180°.

∠КОA = 180° – ∠АОL = 180° – 78° = 102°.

ОК = ОA – радіуси кола. Трикутник КОA – рівнобедрений.

∠ОКA = ∠ОAК.

∠AКL  = ∠AКO = (180° – ∠KOA) =  (180° – 102°) : 2 = 78° : 2 = 39°

Відповідь: ∠AKL = 39°.

 

Завдання 4 Прямі ВК і BL дотикаються до кола із цен­тром О в точках К і L, ∠KBL = 60°. Знайдіть довжину відрізка ВО, якщо радіус кола дорів­нює 8 см.

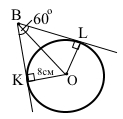
За умовою ВK і BL – дотичні,  ∠BKO = ∠BLO = 90°, катети OK = OL – радіуси кола, ОВ – спільна гіпотенуза, ∆BKO = ∆BLO (за катетом і гіпотенузою). Відповідні кути ∠KBO = ∠LBO, ∠KBL = ∠KBO + ∠LBO = 60°, ∠KBO = 1/2 ∠KBL = 1/2 • 60° = 30°. Звідси KO = 1/2 BO (катет проти кута 30° дорівнює половині гіпотенузи), ВО  = 2КО = 8 см • 2 = 16 см.

Відповідь: 16 см.

 

 

ВАРІАНТ 4

Завдання 1 На якому з малюнків зображено коло, вписане у трикутник?

Коло, вписане у трикутник, дотикається до трьох його сторін.

А (до 2-х сторін)       Б (до жодної)   В (до 3-х сторін)    Г (до 3-х сторін)

 

Завдання 2 Накресліть коло радіуса 21 мм. Проведіть у ньому діаметр АК та хорду CF. Проведіть за допомогою косинця дотичну до кола, що проходить через точку А.

 

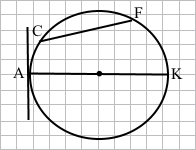
Завдання 3 На малюнку точка О – центр кола, ∠ABM = 38°. Знайдіть ∠AOM.

ОС = ОB – радіуси кола. Трикутник BOM – рівнобедрений.

∠OBM = ∠ABM = ∠OMB.

∠MOB = 180° – 2∠ABM = 180° – 38° • 2 = 104°

Сума суміжних кутів 180°.

∠AOM = 180° – ∠MОB = 180° – 104° = 76°.

Відповідь: ∠AOM = 76°.

 

Завдання 4 З точки А до кола із центром О проведено дотич­ні АВ і АС (В і С – точки  дотику), AO = 18 см, АВ = 9 см. Знайдіть ∠BOC.

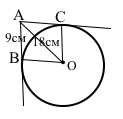
За умовою АО = 18 см, АВ = 9 см, АВ і АС – дотичні,  ∠АВО = ∠АСO = 90°, трикутники АВО і САО – прямокутні. Оскільки катет АВ дорівнює половині гіпотенузи АО, то кут навпроти нього ∠ВОА = 30°.  

Катети ОВ = ОС – радіуси кола, гіпотенуза АО – спільна сторона, ∆ВAO = ∆САО (за катетом і гіпотенузою). Відповідні кути ∠ВОА = ∠СОА = 30°.  ∠ВОС = ∠ВОА + ∠СОА = 30° + 30° = 60°.

Відповідь: ∠ВОС = 60°.