САМОСТІЙНА РОБОТА 1 [1M]

Чотирикутники, паралелограм і його властивості

ВАРІАНТ 1 

Завдання 1  Укажіть фігуру, що є паралелограмом.

Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні.  

А трикутник

Б паралелограм

В чотирикутник

Г чотирикутник

Завдання 2  Знайдіть четвертий кут чотирикутника, якщо три його кути дорів­нюють 70°, 50° і 130°.

Сума кутів чотирикутника дорівнює 360°.

360° – (70° + 50° + 130°) = 110°

Відповідь: 110°.

Завдання 3  У паралелограмі гострий кут дорівнює 60°. Висота паралелограма, проведена з вершини тупого кута, ділить протилежну сторону на відрізки 4 см і 7 см, починаючи від вершини гострого кута. Знай­діть периметр паралелограма.

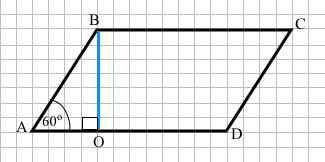
За умовою ∠ВАО = 60°, AO = 4 см, OD = 7 см, ВО – висота до сторони AD, ∠BOA = 90°.

АD = AO + ОD = 4 см + 7 см = 11 см (основна властивість вимірювання відрізків).

∆АВО – прямокутний, ∠АВО = 90° – ∠ВАО = 90° – 60° = 30° (наслідок про суму кутів прямокутного трикутника). Катет навпроти кута 30° дорівнює половині гіпотенузи, тому АВ = АО • 2 = 4 см • 2 = 8 см

Р = 2 • (AD + AB) = 2 • (11 см + 8 см) = 38 см

Відповідь: периметр паралелограма 38 сантиметрів.

Завдання 4  Два кути паралелограма відносяться як 2 : 3. Знайдіть кут між ви­сотами паралелограма, проведеними з вершини тупого кута.

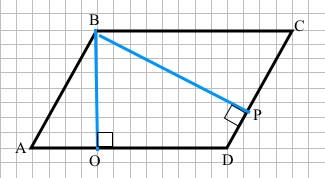
За умовою ABCD – паралелограм, сума двох сусідніх кутів паралелограма дорівнює 180°. 

Нехай х (°) – градусна міра частини кута, 2х (°) – гострий ∠А, 3х (°) – сусідній тупий ∠D. Маємо рівняння. 

2х + 3х = 180

5х = 180

х = 180 : 5

х = (150 + 30) : 5

х = 36

3х = 36 • 3 = 108 (°) – тупий ∠D. 

За умовою ВО – висота до сторони AD, ∠BOD = 90°; ВР – висота до сторони СD, ∠BPD = 90°.  

Чотирикутник OBPD – опуклий, ∠OBP + ∠BPD + ∠D + ∠BOD = 360° (сума кутів чотирикутника), звідси ∠OBP = 360 – ∠BPD – ∠D – ∠BOD = 360°– 90°– 108°– 90°= 72°– шуканий кут між висотами з вершини тупого кута паралелограма. 

Відповідь: 72°.

ВАРІАНТ 2 

Завдання 1 Укажіть паралелограм.

Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні.  

А Чотирикутник (трапеція)

Б Чотирикутник (трапеція)

В Трикутник

Г Паралелограм

Завдання 2 Три кути чотирикутника дорівнюють 70°, 60° і 140°. Знайдіть чет­вертий кут чотирикутника.

Сума кутів чотирикутника дорівнює 360°.

360° – (70° + 60° + 140°) = 90°

Відповідь: 90°.

Завдання 3 У паралелограмі тупий кут дорівнює 120°, а висота, проведе­на з його вершини, ділить протилежну сторону на відрізки 3 см і 4 см, починаючи від вершини тупого кута. Знайдіть периметр па­ралелограма.

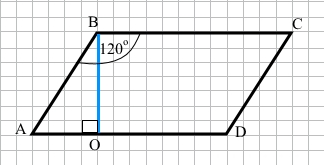
За умовою ∠ABC = 120°, AO = 3 см, OD = 4 см, ВО – висота до сторони AD, ∠BOA = 90°.

АD = AO + ОD = 3 см + 4 см = 7 см (основна властивість вимірювання відрізків).

Відрізок ОВ лежить на січній до прямих AD||BC, звідси ∠ОВС = ∠ВОА = 90° (внутрішні різносторонні кути рівні).

∠АВС = ∠АВО + ∠ОВС (основна властивість вимірювання кутів), звідси ∠АВО = ∠АВС – ∠ОВС = 120° – 90° = 30°.  Катет навпроти кута 30° дорівнює половині гіпотенузи, тому АВ = АО • 2 = 3 см • 2 = 6 см

Р = 2 • (AD + AB) = 2 • (6 см + 10 см) = 32 см

Відповідь: периметр паралелограма 32 сантиметри.

Завдання 4 Кути паралелограма відносяться як 4 : 5. Знайдіть кут між висота­ми паралелограма, проведеними з вершини гострого кута.

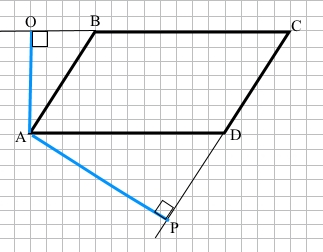
За умовою ABCD – паралелограм, сума двох сусідніх кутів паралелограма дорівнює 180°.

Нехай х (°) – градусна міра частини кута, 4х (°) – гострий ∠С, 5х (°) – сусідній тупий ∠АDС. Маємо рівняння.

4х + 5х = 180

9х = 180

х = 180 : 9

х = 20

4х = 20 • 4 = 80 (°) – гострий ∠C.

За умовою AO – висота до сторони BC, звідси  ∠О = 90°, AР – висота до сторони CD, звідси ∠P = 90°.

AOCP – опуклий чотирикутник, ∠A + ∠O + ∠C + ∠P = 360°

∠A = 360° – ∠O – ∠C – ∠P = 360°– 90°– 80°– 90°= 100°  – шуканий кут між висотами з вершини гострого кута паралелограма. 

Відповідь: 100°.

ВАРІАНТ 3

Завдання 1 Укажіть паралелограм.

Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні.  

А Трикутник

Б Чотирикутник

В Паралелограм

Г Чотирикутник (трапеція)

Завдання 2 Знайдіть четвертий кут чотирикутника, якщо три його кути дорів­нюють 80°, 130° і 90°.

Сума кутів чотирикутника дорівнює 360°.

360° – (80° + 130° + 90°) = 60°

Відповідь: 60°.

Завдання 3 Тупий кут паралелограма дорівнює 120°, а висота, проведена з вер­шини цього кута, ділить протилежну сторону на відрізки 5 см і 3 см, починаючи з вершини гострого кута. Знайдіть периметр паралелограма.

За умовою ∠ABC = 120°, AO = 5 см, OD = 3 см, ВО – висота до сторони AD, ∠BOA = 90°.

АD = AO + ОD = 5 см + 3 см = 8 см (основна властивість вимірювання відрізків).

Відрізок ОВ лежить на січній до прямих AD||BC, звідси ∠ОВС = ∠ВОА = 90° (внутрішні різносторонні кути рівні).

∠АВС = ∠АВО + ∠ОВС (основна властивість вимірювання кутів), звідси ∠АВО = ∠АВС – ∠ОВС = 120° – 90° = 30°.  Катет навпроти кута 30° дорівнює половині гіпотенузи, тому АВ = АО • 2 = 5 см • 2 = 10 см

Р = 2 • (AD + AB) = 2 • (10 см + 8 см) = 36 см

Відповідь: периметр паралелограма 36 сантиметрів.

Завдання 4 Два кути паралелограма відносяться як 7 : 11. Знайдіть кут між висотами паралелограма, проведеними з вершини тупого кута.

За умовою ABCD – паралелограм, сума двох сусідніх кутів паралелограма дорівнює 180°. 

Нехай х (°) – градусна міра частини кута, 7х (°) – гострий ∠А, 11х (°) – сусідній тупий ∠D. Маємо рівняння. 

7х + 11х = 180

18х = 180

х = 180 : 18

х = 10

11х = 11 • 10 = 110 (°) – тупий ∠D. 

За умовою ВО – висота до сторони AD, ∠BOD = 90°; ВР – висота до сторони СD, ∠BPD = 90°.  

Чотирикутник OBPD – опуклий, ∠OBP + ∠BPD + ∠D + ∠BOD = 360° (сума кутів чотирикутника), звідси ∠OBP = 360 – ∠BPD – ∠D – ∠BOD = 360°– 90°– 110°– 90°= 70°– шуканий кут між висотами з вершини тупого кута паралелограма. 

Відповідь: 70°.

ВАРІАНТ 4

Завдання 1 Укажіть фігуру, що є паралелограмом.

Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні.  

А Паралелограм

Б Трикутник

В  Чотирикутник (трапеція)

Г Чотирикутник (трапеція)

Завдання 2 Три кути чотирикутника дорівнюють 100°, 70° і 60°. Знайдіть чет­вертий кут чотирикутника.

Сума кутів чотирикутника дорівнює 360°.

360° – (100° + 70° + 60°) = 130°

Відповідь: 130°.

Завдання 3 Гострий кут паралелограма дорівнює 60°, а висота, проведена з вершини тупого кута, ділить протилежну сторону на відрізки 4 см і 6 см, починаючи з вершини тупого кута. Знайдіть периметр паралелограма.

За умовою ∠ВАО = 60°, AO = 4 см, OD = 6 см, ВО – висота до сторони AD, ∠BOA = 90°.

АD = AO + ОD = 4 см + 6 см = 10 см (основна властивість вимірювання відрізків).

∆АВО – прямокутний, ∠АВО = 90° – ∠ВАО = 90° – 60° = 30° (за наслідком про суму кутів прямокутного трикутника). Катет навпроти кута 30° дорівнює половині гіпотенузи, тому АВ = АО • 2 = 4 см • 2 = 8 см

Р = 2 • (AD + AB) = 2 • (8 см + 10 см) = 36 см

Відповідь: периметр паралелограма 36 сантиметрів.

Завдання 4 Два кути паралелограма відносяться як 13 : 5. Знайдіть кут між висотами, проведеними з вершини гострого кута.

За умовою ABCD – паралелограм, сума двох сусідніх кутів паралелограма дорівнює 180°.

Нехай х (°) – градусна міра частини кута, 5х (°) – гострий ∠С, 13х (°) – сусідній тупий ∠АDС. Маємо рівняння.

5х + 13х = 180

18х = 180

х = 180 : 18 

х = 10

5х = 5 • 10 = 50 (°) – гострий ∠C.

За умовою AO – висота до сторони BC, звідси  ∠О = 90°, AР – висота до сторони CD, звідси ∠P = 90°.

AOCP – опуклий чотирикутник, ∠A + ∠O + ∠C + ∠P = 360°

∠A = 360° – ∠O – ∠C – ∠P = 360°– 90°– 50°– 90°= 130°  – шуканий кут між висотами із вершини гострого кута паралелограма. 

Відповідь: 130°.