ГДЗ зошит Контроль навчальних досягнень (діагностувальні роботи) математика 6 клас Мартинюк (відповіді до підручника Істера)

СДР 10

КОЛО, ДОВЖИНА КОЛА, КРУГ, ПЛОЩА КРУГА, КРУГОВИЙ СЕКТОР, КРУГОВІ ДІАГРАМИ

Варіант 1

Завдання 1  На рисунку зображено діаметр кола АВ, якщо точка О — центр цього кола.

Б

Завдання 2  Знайдіть довжину кола, радіус якого дорівнює 7 см, урахувавши, що π = 3,14.

l = 2πR = 2 • 3,14 • 7 = 43,96 (см)

А 42 см             Б 21,98 см              В 43,96 см                Г 153,86 см

Завдання 3  Клумба має форму круга, радіус якого дорівнює 4 м. Скільки декоративних рослин можна на ній посадити, якщо для кожної з них потрібно виділити ділянку площею 0,16 м²? Врахувати, що π =3,14.

R — 4 м

S — ? р. — ? м²

       1 р. — 0,16 м²

Розв’язання

1) S = πR² = 3,14 • 4² = 50,24 (м²) – площа ділянки.  

2) 50,24 : 0,16 = 314 (р.)

Відповідь: можна посадити 314 декоративних рослин.

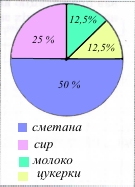
Завдання 4 Орися заплатила за покупку 360 грн. За 90 грн вона придбала сир, 50% коштів витра­тила на купівлю сметани, 45 грн заплатила за молоко, а за решту купила цукерки. На­рисуй кругову діаграму витрат дівчинки (у %).

С. — 90 грн

См. — 50% від 360 грн

М. — 45 грн

Ц. — решта

Разом — 360 грн

Розв’язання

1) 360 • 0,5 = 180 (грн) – заплатила за сметану.

2) 360 – (90 + 45 + 180) = 45 (грн) – заплатила за цукерки. 

3) 90 : (360 : 100) = 25 (%) – витратила за сир. 

4) 180 : (360 : 100) = 50 (%) – витратила за сметану. 

5) 45 : (360 : 100) = 12,5 (%) – витратила за молоко або цукерки. 

Відповідь: сир 25%, сметана 50%, молоко 12,5%, цукерки 12,5%

Переводимо гривні у відсотки

Обчислення градусних мір кругових секторів для побудови діаграми 

Варіант 2

Завдання 1  На рисунку зображено круговий сектор, якщо точка О — центр цього кола.

А

Завдання 2  Знайдіть довжину кола, діаметр якого дорівнює 6 см, урахувавши, що π = 3,14.

l = 2πR = 2 • 3,14 • 6 = 37,68 (см)

А 226,08 см            Б 113,04 см          В 37,68 см             Г 18,84 см

Завдання 3  Підлогу астрономічної обсерваторії у формі круга діаметра 10 м потрібно пофарбувати. Скільки літрів фарби потрібно закупити, якщо розхід на 1 м² підлоги становить 0,2 л? Врахувати, що π = 3,14.

d — 10 м

S — ? м² —  ? л

       1 м² — 0,2 л

Розв’язання

1) R = d : 2 = 10 : 2 = 5 (м) – радіус круга.

2) S = πR² = 3,14 • 5² = 78,5 (м²) – площа ділянки.  

3) 78,5 • 0,2 = 15,7 (л)

Відповідь: потрібно купити 15,7 літрів фарби.

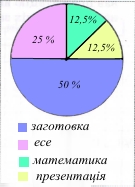
Завдання 4  Микола витратив на виконання домашніх завдань 4 год. Задачі з математики він розв'язував 30 хв, есе з української мови писав 25% усього часу, дерев'яну заготовку для ручки напилка на урок трудового навчання виготовляв 2 год, а решту часу створю­вав презентацію на урок інформатики. Нарисуй кругову діаграму розподілу часу вико­нання домашніх завдань (у %).

М. — 30 хв = 0,5 год

Ес. — 25% від 4 год

З. — 2 год

Пр. — решта

Разом — 4 год

Розв’язання

1) 4 • 0,25 = 1 (год) – час на есе.  

2) 4 – (0, 5 + 1 + 2) = 0,5 (год) – час на презентацію.  

3) 0,5 : (4 : 100) = 12,5 (%) – час на математику або презентацію. 

4) 1 : (4 : 100) = 25 (%) – час на есе. 

5) 2 : (4 : 100) = 50 (%) – час на заготовку. 

Відповідь: математика 12,5%, есе 25%, заготовка 50%, презентація 12,5%

Переводимо час у відсотки

Обчислення градусних мір кругових секторів для побудови діаграми