ГДЗ Бліцоцінювання відривні картки математика 5 клас Мартинюк у 2-х частинах за програмою Істера

Бліцоцінювання № 21

Рівняння 

Варіант 1

Завдання 1   

Зх + 5 = 14

3х = 14 – 5

3х = 9

х = 9 : 3 

х = 3 

Відповідь: 3 – корінь рівняння. 

Завдання 2 

Завдання 3 У господині було 164 кг яблук. Вона приготувала варення, а з 64 кг — сік, після чого в неї залишило­ся 78 кг яблук. Скільки кілограмів яблук витрати­ла господиня на приготування варення?

Було — 164 кг

Варення — ?

Сік — 64 кг

Залишилось — 78 кг

Розв’язання

1) 164 – 78 = 164 – 100 + 22 = 86 (кг) – на приготування варення і соку.   

2) 86 – 64 = 22 (кг) 

Відповідь: на приготування варення витратила 22 кілограми яблук. 

Варіант № 2

Завдання 1 

2х – 4 = 14

2х = 14 + 4

2х = 18

х = 18 : 2 

х = 9

Відповідь: 9 – корінь рівняння. 

Завдання 2 

Завдання 3

У ємності було 189 л розчину для проведення обробки сільсько­господарських угідь. Для першого поля використали 56 л роз­чину. Після обробки другого поля у ємності залишилося 46 л розчину. Скільки літрів розчину використали для обробки дру­гого поля?

Було — 189 л

І п. — 56 л

ІІ п. — ? л

Залишилось — 46 л

Розв’язання

1) 189 – 46 = 143 (л) – розчину використали.    

2) 143 – 56 = 143 – 43 – 13 = 87 (л) 

Відповідь: для обробки другого поля використали 87 літрів розчину.  

Бліцоцінювання № 22

Рівняння

Варіант № 1

Завдання 1  Двоє мотоциклістів вирушили одночасно з однієї точки в протилежних напрямках. Швидкість руху першого мотоцикліста становить 45 км/год, а дру­гого — 50 км/год. Якою буде відстань між мотоциклістами через 2 год?

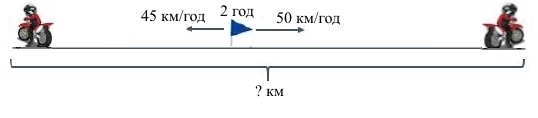
Розв’язання

1) 50 + 45 = 95 (км/год) – швидкість віддалення.  

2) 95 • 2 = (90 + 5) • 2 = 190 (км) 

Відповідь: відстань буде 190 кілометрів.   

Завдання 2 Моторний човен, власна швидкість якого 26 км/год, рухав­ся 3 год за течією річки і 4 год проти течії річки. Яку від­стань він подолав, якщо швидкість течії річки 2 км/год?

За течією — 3 год зі швидкістю 26 + 2 км/год

Проти течії — 4 год зі швидкістю 26 – 2 км/год

Всього — ? км

Розв’язання

1) 26 + 2 = 28 (км/год) – швидкість за течією річки.

2) 28 • 3 = (20 + 8) • 3 = 78 (км) – відстань за течією річки. 

3) 26 – 2 = 24 (км/год) – швидкість проти течії річки. 

4) 24 • 4 = (20 + 4) • 4 = 96 (км) – відстань проти течії річки. 

5) 78 + 96 = 160 + 14 = 174 (км)

Відповідь: подолав відстань 174 кілометри. 

Завдання 3  Із Тернополя до Києва одночасно виїхали вантажний і легковий автомобілі. Через 4 год відстань між ними ста­новила 48 км. Знайдіть швидкість легкового автомобі­ля, якщо відомо, що швидкість вантажівки дорівнює 65 км/год і вона менша за швидкість легковика.

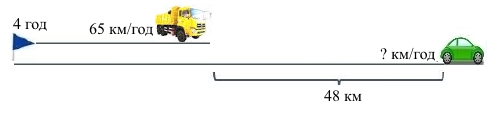
Розв’язання

1) 65 • 4 = (60 + 5) • 4 = 260 (км) – відстань вантажівки.

2) 260 + 48 = 308 (км) – відстань автомобіля. 

3) 308 : 4 = (280 + 28) : 4 = 77 (км/год)

Відповідь: швидкість легкового автомобіля 77 км/год.  

Варіант № 2

Завдання 1  Двоє велосипедистів вирушили назустріч один одному з двох міст. Швидкість руху першого з них дорівнює 13 км/год, а другого — 15 км/год. Через 5 год вони зустрілися. Яка відстань між містами?

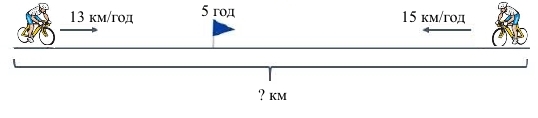
Розв’язання

1) 13 + 15 = 28 (км/год) – швидкість віддалення.  

2) 28 • 5 = (20 + 8) • 5 = 140 (км) 

Відповідь: відстань між містами 140 кілометрів.   

Завдання 2 Човен на підводних крилах, власна швидкість якого 35 км/год, рухався 2 год за течією і 5 год проти течії річки. Яку відстань він подолав, якщо швидкість течії річки 3 км/год?

За течією — 2 год зі швидкістю 35 + 3 км/год

Проти течії — 5 год зі швидкістю 35 – 3 км/год

Всього — ? км

Розв’язання

1) 35 + 3 = 38 (км/год) – швидкість за течією річки.

2) 38 • 2 = (30 + 8) • 2 = 76 (км) – відстань за течією річки. 

3) 35 – 3 = 32 (км/год) – швидкість проти течії річки. 

4) 32 • 5 = (30 + 2) • 5 = 160 (км) – відстань проти течії річки. 

5) 76 + 160 = 160 + 14 = 174 (км)

Відповідь: подолав відстань 174 кілометри. 

Завдання 3 Автобус був у дорозі 6 год, а вантажний автомобіль — 4 год. Автобус подолав на 156 км більше, ніж автомо­біль. Яку відстань подолали автобус і вантажівка разом, якщо їхні швидкості однакові?

Розв’язання

1) 6 – 4 = 2 (год) – на стільки більше годин у дорозі автобус.

2) 156 : 2 = (140 + 16) : 2 = 78 (км/год) – швидкість автобуса (вантажівки). 

3) 78 • 4 = (70 + 8) • 4 = 312 (км) – відстань вантажівки. 

4) 312 + 156 = 468 (км) – відстань автобуса. 

5) 312 + 468 = 780 (км)

Відповідь: разом подолали 780 кілометрів.