ГДЗ робочий зошит Математика 4 Скворцова, Онопрієнко (відповіді) НУШ

ГДЗ Математика 4 клас

04.10.2025

РОЗВ’ЯЗУЄМО СКЛАДЕНІ ЗАДАЧІ З ВЕЛИЧИНАМИ: ПОДОЛАНИЙ ШЛЯХ, ШВИДКІСТЬ РУХУ, ЧАС РУХУ

Завдання 241

► 1) Лижник біг за вітром 2 год зі швидкістю 15 км/год, а коли біг назад, проти вітру, той самий шлях він подолав зі швидкістю 10 км/год. Скільки часу лижник витратив на зворотний шлях?

t₁ — 2 год

v₁ — 15 км/год

v₂ — 10 км/год

t₂ — ? год

Розв’язання

1) s = v₁ • t₁ = 15 • 2 = 30 (км) – відстань.

2) t₂ = s : v₂ = 30 : 10 = 3 (год)

Відповідь: на зворотний час витратив 3 години.

► 2) Лижник біг за вітром 2 год зі швидкістю 15 км/год, а коли біг назад, проти вітру, той самий шлях він подолав зі швидкістю, що була на 5 км/год меншою. Скільки часу лижник витратив на зворотний шлях?

t₁ — 2 год

v₁ — 15 км/год

v₂ — на 5 км/год менша

t₂ — ? год

Розв’язання

1) s = v₁ • t₁ = 15 • 2 = 30 (км) – відстань.

2) 15 – 5 = 10 (км/год) – швидкість на зворотному шляху.

3) t₂ = s : v₂ = 30 : 10 = 3 (год)

Відповідь: на зворотний час витратив 3 години.

Завдання 242

10 000 + а = 711 000 – 1 000

10 000 + а = 710 000

а = 710 000 – 10 000

а = 700 000

(404 080 – 4 000) – х = 80

400 080 – х = 80

х = 400 080 – 80

х = 400 000

Завдання 243

(37 : 1) + (0 : 868) + (4200 : 1) – (1 • 37) = 37 + 0 + 4 200 – 37 = 4 200

1) 37 : 1 = 37

2) 0 : 868 = 0

3) 4 200 : 1 = 4 200

4) 1 • 37 = 37

5) 37 + 0 = 37

6) 37 + 4 200 = 4 237

6) 4 237 – 37 = 4 200

ПОВТОРЮЄМО ВИВЧЕНЕ

Завдання 244

► 1) Велосипедист і велосипедистка тренувалися однаковий час. Велосипедист проїхав 90 км, а велосипедистка, рухаючись гірською трасою, — З0 км. З якою швидкістю рухалася велосипедистка, якщо швидкість руху велосипедиста становила 15 км/год?

s₁ — 90 км

v₁ — 15 км/год

s₂ — 30 км

v₂ — ? км/год

t₁ — t₂

Розв’язання

1) t = s₁ : v₁ = 90 : 15 = 90 : 3 : 5 = 6 (год) – час тренування.

2) v₂ = s₂ : t = 30 : 6 = 5 (км/год)

Відповідь: велосипедистка їхала зі швидкістю 5 км/год.

► 2) Велосипедист і велосипедистка тренувалися однаковий час. Велосипедист проїхав 90 км, а велосипедистка, рухаючись гірською трасою, подолала третину цієї відстані. З якою швидкістю рухалася велосипедистка, якщо швидкість руху велосипедиста становила 15 км/год?

s₁ — 90 км

v₁ — 15 км/год

s₂ — 1/3 від 90 км

v₂ — ? км/год

t₁ — t₂

Розв’язання

1) t = s₁ : v₁ = 90 : 15 = 90 : 3 : 5 = 6 (год) – час тренування.

2) 90 : 3 = 30 (км) – шлях велосипедистки.

3) v₂ = s₂ : t = 30 : 6 = 5 (км/год)

Відповідь: велосипедистка їхала зі швидкістю 5 км/год.

Завдання 245 Виконай множення письмово.

х635

2540

х278

1668

х427

3416

х205

1845

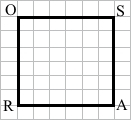
Завдання 246 Обчисли периметр прямокутника зі сторонами 25 мм і 35 мм. Побудуй квадрат ROSA з тим самим периметром.

а — 25 мм

b — 35 мм

Р — ?

Розв’язання

1) Р = (25 + 35) • 2 = 60 • 2 = 120 (мм) = 12 (см)

2) 12 : 4 = 3 (см) – сторона квадрата ROSA.

ВИВЧАЄМО ГЕОМЕТРИЧНІ ФІГУРИ НА ПЛОЩИНІ

Завдання 247 У трикутнику ABC кут В — прямий, ВА = 3 см, ВС = 4 см. Побудуй трикутник ABC. Виміряй сторону АС. Знайди периметр трикутника ABC.

АС = 5 см

План побудови прямокутного трикутника.

1) Побудуй прямий кут В.

2) На одній стороні прямого кута відклади відрізок ВА завдовжки 3 см.

3) На іншій стороні прямого кута відклади відрізок ВС завдовжки 4 см.

4) З'єднай кінці побудованих відрізків.

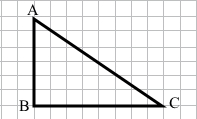
Р = 3 см + 4 см + 5 см = 12 см

Завдання 248 Постав дужки, щоб одержати істинні рівності.

(1 000 + 200) : 2 : 50 = 1200 : 2 : 50 = 600 : 50 = 60 : 5 = 12

(19 000 – 9 000) : 100 : 10 = 10 000 : 100 : 10 = 100 : 10 = 10

4 000 – (500 : 100) = 4 000 – 5 = 3995

(21 + 934 – 655) : 100 = (955 – 655) : 100 = 300 : 100 = 3

Завдання 249

6 598 + 10 404 + 17 883 = 17 002 + 17 883 = 34 885

+10404

6508

17002

+17002

17883

34885

24 702 – 1 438 + 946 = 23 264 + 946 = 24 210

_24702

1438

23264

+23264

946

24210

24 702 – (1438 + 946) = 24 702 – 2 384 = 22 318

+1468

946

2384

_24702

2384

22318

5 830 + 70 898 + 5 708 = 76 728 + 5 708 = 82 436

+70898

5830

76728

+76728

5708

82436

60 726 – 2 581 + 1 806 = 58 145 + 1 806 = 59 951

_60726

2581

58145

+58145

1806

59951

802 620 – (20 000 – 4 634) + 64 589 = 802 620 – 15 366 + 64 589 = 787 254 + 64 589 = 851 843

_20000

4634

15366

_802620

15366

787254

+787254

64589

851843

Завдання 250 Виконай перевірку.

(346 + t) = 463 + 128

346 + t = 591

t = 591 – 346

t = 245

346 + 245 = 591

463 + 128 = 591

591 = 591

91 – (b + 46) = 8 + 12

91 – (b + 46) = 20

b + 46 = 91 – 20

b + 46 = 71

b = 71 – 46

b = 25

91 – (25 + 46) = 91 – 71 = 20

8 + 12 = 20

20 = 20

Завдання 251

► У три зали кінотеатру всього продали 470 білетів, причому в першу та другу залу разом продали 310 білетів, а в другу і третю — 290 білетів. Скільки білетів продали в кожну залу кінотеатру окремо?

І,ІІ — 310 б.

ІІ,ІІІ — 290 б.

І,ІІ,ІІІ — 470 б.

І —? б.

ІІ — ? б.

ІІІ — ? б.

Розв’язання

1) 470 – 290 = 180 (б.) – у І залу.

2) 310 – 180 = 130 (б.) – у ІІ залу.

3) 470 – 310 = 160 (б.) – у ІІІ залу.

Відповідь: І – 180 білетів, ІІ – 130 білетів, ІІІ – 160 білетів.

ВИВЧАЄМО ГЕОМЕТРИЧНІ ФІГУРИ НА ПЛОЩИНІ

Завдання 252 Визнач види кутів у многокутнику на малюнку.

Тупі кути (> 90°): M, K, P, N.

Гострі кути (< 90°): L.

Прямі кути (= 90°): O.

Завдання 253

► 1) Периметр трикутника, у якого всі сторони рівні, становить 51 мм. Знайди довжину сторони трикутника.

Рівносторонній трикутник — трикутник, у якого всі сторони рівні.

Сторона — ? мм

Р — 51 мм

Розв’язання

51 : 3 = (30 + 21) : 3 = 17 (мм) – сторона рівностороннього трикутника.

► 2) Периметр трикутника, у якого дві сторони рівні, становить 50 мм, а довжина однієї зі сторін дорівнює 18 мм. Знайди довжини решти сторін трикутника.

І варіант.

І,ІІ — 2 рази по 18 мм

ІІІ — ? мм

Р — 50 мм

Розв’язання

1) 18 • 2 = 36 (мм) – сума рівних сторін.

2) 50 – 36 = 14 (см) – ІІІ сторона.

Відповідь: 18 см і 14 см.

ІІ варіант

І,ІІ — 2 рази по ? мм

ІІІ — 18 мм

Р — 50 мм

Розв’язання

1) 50 – 18 = 32 (мм) – сума рівних сторін.

2) 32 : 2 = (20 + 12) : 2 = 16 (см) – І (ІІ) сторона.

Відповідь: 16 см і 16 см.

► 3) Периметр трикутника, у якого всі сторони різної довжини, становить 104 мм. Довжина однієї зі сторін трикутника дорівнює 46 мм, довжина другої сторони становить половину довжини першої. Знайди довжину третьої сторони трикутника.

І — 46 мм

ІІ — 1/2 від 46 мм

ІІІ — ?

Р — 104 мм

Розв’язання

1) 46 : 2 = 23 (мм) – ІІ сторона.

2) 46 + 23 = 69 (мм) – І і ІІ разом.

3) 104 – 69 = 35 (мм) – ІІІ сторона.

Відповідь: довжина третьої сторони 35 мм.

Завдання 254

Тіло	Швидкість (км/год)	Час (год)	Шлях (км)
Легковик	100	5	500
Вантажівка	65	7	455
Лижник	5	4	60
Вертоліт	280	3	840
Потяг	64	5	320
Пішохід	4	4	16

1) 500 : 100 = 5 (год) – час легковика.

2) 65 • 7 = 455 (км) – шлях вантажівки.

3) 60 : 4 = 5 9км/год) – швидкість лижника.

4) 840 : 280 = 3 (год) – час вертольота.

5) 64 • 5 = 320 (км) – шлях потяга.

6) 16 : 4 = 4 (км/год) – швидкість пішохода.

Завдання 255

(56 728 + 997) – (324 : 6 • 17 + 7 324) = 49 483

1) 56 728 + 997 = 56 728 + 1 000 – 3 = 57 725

2) 324 : 6 = (300 + 24) : 6 = 50 + 4 = 54

3) 54 • 17 = 918

4) 918 + 7 324 = 8 242

5) 57 725 – 8 242 = 49 483

307 003 – (4 625 + 9 999) – 99 996 + 5 822 = 198 205

1) 4 625 + 9 999 = 4 625 + 10 000 – 1 = 14 624

2) 307 003 – 14 624 = 292 379

3) 292 379 – 99 996 = 292 379 – 100 000 + 4 = 192 383

4) 192 383 + 5 822 = 198 205

ВИВЧАЄМО ГЕОМЕТРИЧНІ ФІГУРИ В ПРОСТОРІ

Завдання 256

Циліндр, куб, куля, піраміда, конус, паралелепіпед.

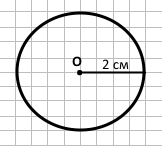
Завдання 257 Накресли коло діаметром 8 см із центром у точці О. Накресли коло із центром у точці Р, радіус якого у 2 рази менший, ніж радіус першого кола.

8 : 2 = 4 (см) – радіус першого кола.

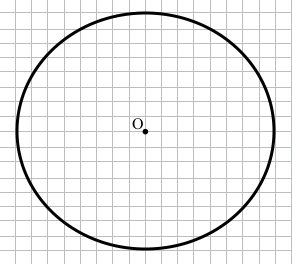
4 : 2 = 2 (см) – радіус другого кола.

Завдання 258

Швидкість, v	Час, t	Відстань, s
8 м/с	8 с	8 м/с • 8 с = 64 м
72 км : 6 год = 12 км/год	6 год	72 км
320 км : 40 хв = 8 км/хв	40 хв	320 км
8 м/хв	560 м : 8 м/хв = 70 хв	560 м

Завдання 259

► Лижниця за б год подолала 72 км, а хлопець на снігоході за 2 год проїхав 100 км. Чия швидкість руху була більшою? На скільки більшою?

Л. — 72 км за 6 год

Хл. — 100 км за 2 год

Швидкість — на ? км/год більша

Розв’язання

1) 72 : 6 = (60 + 12) : 6 = 12 (км/год) – швидкість лижниці.

2) 100 : 2 = 50 (км/год) – швидкість на снігоході.

3) 50 – 12 = 38 (км/год)

Відповідь: на 38 км/год швидкість на снігоході більша.

Завдання 260

11 763 – b = 8 894

b = 11 763 – 8 894

b = 2869

a – 783 001 = 96 000

a = 96 000 + 783 001

a = 879 001

168 : с = 21

c = 168 : 21

c = 8

p – 84 235 = 76 567

p = 76 567 + 84 235

p = 160 802

142 • k = 994

k = 994 : 142

k = 7

n : 280 = 7

n = 7 • 280

n = 1 960

Завдання 261 Заміни прості іменовані числа складеними.

1 кг = 1000 г, 1 ц = 100 кг

1 м = 10 дм = 100 см, 1 дм = 10 см

1 км = 1 000 м = 10 000 дм

4 638 г = 4 000 г + 638 г = 4 кг 638 г

245 см = 200 см + 45 см = 2 м 45 см

429 ц = 420 ц + 9 ц = 42 т 9 ц

18 907 м = 18 000 м + 907 м = 18 км 907 м

1 930 г = 1 000 г + 930 г = 1 кг 930 г

23 656 дм = 20 000 дм + 3 650 дм + 6 дм = 2 км 365 м 6 дм

УЗАГАЛЬНЮЄМО ЗНАННЯ ПРО АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ І ДІЛЕННЯ

Завдання 262

17 • 10 • 2 = 17 • 2 • 10 = 34 • 10 = 340

50 • 35 • 2 = 50 • 2 • 35 = 100 • 35 = 3 500

5 • 7 • 6 = 5 • 6 • 7 = 30 • 7 = 210

5 • 8 • 9 • 2 = (5 • 2) • (8 • 9) = 10 • 72 = 720

(72 + 36) : 12 = 72 : 12 + 36 : 12 = 6 + 3 = 9

(144 – 72) : 18 = 72 : 18 = 4

80 : (2 • 8) = 80 : 8 : 2 = 10 : 2 = 5

12 • 20 • 4 = 12 • 80 = 960

8 • 5 • 16 = 40 • 16 = 640

22 • 6 • 5 = 22 • 30 = 660

4 • 9 • 7 • 25 = (4 • 25) • (9 • 7) = 100 • 63 = 6 300

(8 + 9) • 7 = 56 + 63 = 119

(42 • 13) : 14 = 42 : 14 • 13 = 3 • 13 = 39

112 : (4 • 4) = 112 : 16 = 7

Завдання 263

► Мотоцикліст рухався в 5 разів швидше, ніж велосипедист, і за 3 год проїхав 240 км. Скільки кілометрів подолав велосипедист за 2 год?

s₁ — 240 км

t₁ — 3 год

v₂ — у 5 разів більше за v₁

t₂ — 2 год

s₂ — ? км

Розв’язання

1) v₁ = s₁ : t₁ = 240 : 3 = 80 (км/год) – швидкість мотоцикліста.

2) 80 : 5 = (50 + 30) : 5 = 16 (км/год) – швидкість велосипедиста.

3) s₂ = v₂ • t₂ = 16 • 2 = 32 (км)

Відповідь: велосипедист подолав 32 кілометри.

Завдання 264

► Периметр трикутника, у якого дві сторони рівні, дорівнює 58 см. Довжина третьої сторони 12 см. Знайди довжини інших сторін?

АО = АВ

ОВ = 12 см

AO — ? см

Р = 58 см

Розв’язання

1) 58 – 12 = 46 (см) – сума однакових довжин.

2) 46 : 2 = 23 (см)

Відповідь: 23 см і 23 см.

Завдання 265

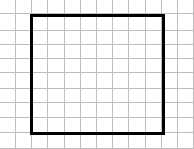
Накресли квадрат ADBK із периметром 16 см.

16 : 4 = 4 (см) – сторона квадрата.

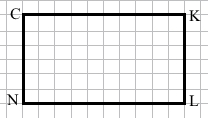
Накресли прямокутник NCKL із тим самим периметром.

16 : 2 = 8 (см) – сума довжини і ширини прямокутника.

8 см = 7 см + 1 см

8 см = 6 см + 2 см

8 см = 5 см + 3 см

Завдання 266

50 – (600 • 3) : (4 • 25) – 5 • (40 – 7 • 5) = 7

1) 600 • 3 = 1800

2) 4 • 25 = 4 • 100 : 4 = 100

3) 7 • 5 = 35

4) 40 – 35 = 5

5) 1800 : 100 = 18

6) 5 • 5 = 25

7) 50 – 18 = 50 – 20 + 2 = 32

8) 32 – 25 = 32 – 30 + 5 = 7

(80 • 8 + 420 : 7) : 100 + (140 : 20 + 38 : 19) • 3 = 34

1) 80 • 8 = 640

2) 420 : 7 = 60

3) 640 + 60 = 700

4) 140 : 20 = 14 : 2 = 7

5) 38 : 19 = 2

6) 7 + 2 = 9

7) 700 : 100 = 7

8) 9 • 3 = 27

9) 7 + 27 = 27 + 3 + 4 = 34

МНОЖИМО БАГАТОЦИФРОВЕ ЧИСЛО НА ОДНОЦИФРОВЕ ПИСЬМОВО

Завдання 267

х567

1701

х3567

10701

х43567

130701

567 • 3 = 1 701

3 567 • 3 = (3 000 + 567) • 3 = 3000 • 3 + 567 • 3 = 9 000 + 1 701 = 10 701

43 567 • 3 = (40 000 + 3 000 + 567) • 3 = 120 000 + 9 000 + 1 701 = 130 701

Завдання 268 Цифр буде в кожному добутку, перевір припущення.

7 309 • 6 ≈ 7 000 • 6 = 42 000 (5 цифр)

23 607 • 4 ≈ 20 000 • 4 = 80 000 (5 цифр)

300 654 • 3 ≈ 300 000 • 3 = 900 000 (6 цифр)

х7309

43854

х23607

94928

х300654

901962

Завдання 269

► 1) Сергій і Олег купили 6 комп'ютерних дисків за однаковою ціною й заплатили 72 грн. Визнач ціну диска.

72 грн — 6 д. по ? грн

Розв’язання

1) 72 : 6 = (60 + 12) : 6 = 12 (грн) – ціна диска.

Відповідь: ціна диска 12 гривень.

► 2) Сергій і Олег купили за однаковою ціною диски: Сергій — 4, а Олег — 2 диски. Усього хлопці заплатили 72 грн. Визнач ціну диска.

С. — 4 д.

Ол. — 2 д.

Разом — 72 гр — ? д. по ? грн

Розв’язання

1) 4 + 2 = 6 (д.) – купили дисків.

2) 72 : 6 = (60 + 12) : 6 = 12 (грн) – ціна диска.

Відповідь: ціна диска 12 гривень.

ДОДАТКОВІ ЗАВДАННЯ

Завдання 270

► Для повного розкладання в природі пластикової пляшки потрібно 450 років, алюмінієвої банки — до 500 років, термін розкладання природного матеріалу (скла) може тривати до 4000 років.

Матеріал	Термін розкладання (у роках)
Скло	4000
Пластик	450
Алюміній	500

Завдання 271 Кількість вуглекислого газу, який поглинають дерева (у кг).

Дерево	1 дерево	5 дерев	20 дерев
Ялина	6	6 • 5 = 30	6 • 20 = 120
Тополя	200 : 5 = 40	200	40 • 20 = 800
Сосна	200 : 20 = 10	10 • 5 = 50	200
Липа	80 : 5 = 16	80	16 • 20 = 320
Дуб	28	28 • 5 = 290	28 • 20 = 360

Завдання 272

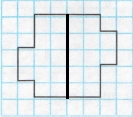
а) Проведи лінії так, щоб розділити фігуру на 2 однакові частини.

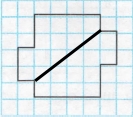
б) Проведи лінії так, щоб розділити фігуру на 4 однакові частини.

Завдання 273 Уперше парк із тваринами стали називати зоопарком у 1451 році в Німеччині. Визнач, скільки років минуло від того часу.

Нехай тепер 2025 рік.

_2025

1451

574 (р.)

Відповідь: минуло 574 роки.

Завдання 274 Розташуй чотирикутники, п'ятикутники, круги і трикутники так, щоб у кожному стовпчику, у кожному рядку, а також у кожному квадраті були всі чотири фігури.

круг	3-кутник	5-кутник	4-кутник
4-кутник	5-кутник	3-кутник	круг
3-кутник	круг	4-кутник	5-кутник
5-кутник	4-кутник	круг	3-кутник

Завдання 275 Усередині кожної із трьох блакитних коробок містяться дві жовті коробки, а в кожній жовтій коробці розташована маленька біла коробка. Скільки всього коробок?

Міркуємо так.

3 (великі коробки) + 3 • 2 (жовті коробки) + 6 (білі коробки)

3 + 3 • 2 + 6 = 3 + 6 + 6 = 15 (к.)

Відповідь: 15 коробок.

Завдання 276 З'ясуй, скільки прямокутників на рисунку.

Х	Х
Х	Х
Х	Х

Відповідь: 18.

Завдання 277 Які три однакові числа треба додати до 50, щоб одержати 500?

Міркуємо так.

500 – 50 = 450 – сума трьох однакових чисел.

450 : 3 = (300 + 150) : 3 = 150 – шукане число.

ІІ спосіб

Складемо рівняння.

50 + (х • 3) = 500

х • 3 = 500 – 50

х • 3 = 450

х = 450 : 3

х = 150

Відповідь: 150, 150, 150.

1 2 3 4 5 6 7 8 9 10