ГДЗ Бліцоцінювання відривні картки математика 5 клас Мартинюк у 2-х частинах за програмою Істера

Бліцоцінювання № 50

Порівняння звичайних дробів з однаковими знаменниками

Варіант 1

Завдання 1 Порівняйте дроби.

Для дробів з однаковими знаменниками у більшого дробу більший чисельник.

511 > 311        1219 < 1419         1741 > 1341

 

Завдання 2  Накресліть координатний промінь, узявши за одиничний відрізок 13 клітинок. Позначте на цьому промені числа 513, 113, 713, 1113. 

 

 

  

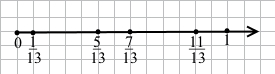
Завдання 3  Знайдіть усі натуральні значення х, для яких правильною є нерівність

1221 < х21 < 1621  Напишіть усі одержані правильні нерівності.

1221 < 1321 < 1621

1221 < 1421 < 1621

1221 < 1521 < 1621

 

 

Варіант 2

Завдання 1 Порівняйте дроби.

Для дробів з однаковими знаменниками у більшого дробу більший чисельник.

713 > 513     2125 < 2325         37146 < 73146

 

 

Завдання 2  Накресліть координатний промінь, узявши за одиничний відрізок 11  клітинок. Позначте на цьому промені числа 511, 111, 711, 911. 

 

 

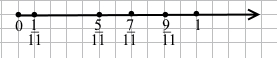
Завдання 3  Знайдіть усі натуральні значення х, для яких правильною є нерівність

1929 < у29 < 2329 

1929 < 2029 < 2329

1929 < 2129 < 2329

1929 < 2229 < 2329

 

 

  

 

Бліцоцінювання 51

Правильні та неправильні дроби

Варіант 1

Завдання 1   Порівняйте дроби.

Для дробів з однаковими знаменниками у більшого дробу більший чисельник. 

1939 < 2939            

5479 < 7979   (правильний дріб менший за неправильний дріб)

1 > 5367          (6767 > 5367)

 

 

Завдання 2  Запишіть усі натуральні значення у, для яких дроби у20 і 13у є одночасно правильними.

У правильного дробу чисельник менший за знаменник: 

для дробу у20 маємо у < 20, для дробу 13у маємо у > 13. 

 

13 < у < 20

Відповідь: у = 14, 15, 16, 17, 18, 19. 

 

Завдання 3  У першому ящику 24 кг картоплі, у другому — 118 цієї кількості, а в третьому — 56 картоплі, що є в першому ящику. Скільки кілограмів картоплі у трьох ящиках разом?

І — 24 кг

ІІ — 118 від 24 кг

ІІІ — 56 від 24 кг

 

Всього — ? кг

Розв’язання

1) 24 : 8 •  11 = 33 (кг) – у ІІ ящику.   

2) 24 : 6 • 5 = 20 (кг) – у ІІІ ящику.

3) 24 + 33 + 20 = 77 (кг)

Відповідь: разом 77 кілограмів картоплі. 

 

Варіант 2

Завдання 1 Порівняйте дроби.

Для дробів з однаковими знаменниками у більшого дробу більший чисельник. 

1727 < 2527            

3859 < 5959   (правильний дріб менший за неправильний дріб)

8153 > 1          (8153 > 5353)

 

 

Завдання 2  Запишіть усі натуральні значення х, для яких дроби х19 і 12х є одночасно правильними.  

У правильного дробу чисельник менший за знаменник:

для дробу х19 маємо х < 19, для дробу 12х маємо х > 12. 

 

 

12 < х < 19

Відповідь: х = 13, 14, 15, 16, 17, 18. 

 

Завдання 3  Мама заплатила за абрикоси 36 грн, за персики — 139 цієї вартості, а за виноград — 911 вартості абрикосів і персиків разом. Скільки заплатила мама за всю покупку?

Абр. — 36 грн

П. — 139 від 36 грн

В. — 911 від абр. і. п. разом

 

Всього — ? кг

Розв’язання

1) 36 : 9 • 13 = 52 (грн) – за персики.   

2) 36 + 52 = 88 (грн) – за абрикоси і персики разом. 

3) 88 : 11 • 9 = 72 (грн) – за виноград.  

4) 36 + 52 + 72 = 160 (грн)

Відповідь: за покупку заплатила 160 гривень.  

 

 

  

Бліцоцінювання № 52

Мішані числа

Варіант 1

Завдання 1  Запишіть мішані числа у вигляді дробів.

а) 317 = 3 • 7 + 1 7 = 227

б) 1223 = 12 • 3 + 2 3 = 383

в) 1357 = 13 • 7 + 5 7 = 967

 

 

Завдання 2  Запишіть неправильний дріб у вигляді мішаного числа. 

а) 187 = 447	_18 | 7    14    2    4  (ост.)
б) 13412 = 11212	_134 | 12   12     11   _14     12       2 (ост.)

 

Завдання 3  Перший мотоцикліст проїхав 1345 м за 1 хв 25 с, а дру­гий — 3510 м за 3 хв 54 с. У котрого з них більша швид­кість руху?

Розв’язання

1 хв 25 с = 60 с + 25 с = 85 с

3 хв 54 с = 60 • 3 + 54 = 234 с

1)_1345 | 85        85     15 (м/с) – швидкість першого мотоцикліста.      _495        425          70 (ост.)

2)_3510 | 234      234     15 (м/с) – швидкість другого мотоцикліста.    _1170      1170            0

Відповідь: більша швидкість першого мотоцикліста.

 

Варіант 2

Завдання 1 Запишіть мішані числа у вигляді дробів.

а) 213 = 2 • 3 + 1 3 = 73

б) 658 = 6 • 8 + 5 8 = 538

в) 1249 = 12 • 9 + 4 9 = 1129

 

 

Завдання 2  Запишіть неправильний дріб у вигляді мішаного числа. 

а) 175 = 325	_17 | 5    15    3     2  (ост.)
б) 12713 = 91013	_127 | 13   117     11     10 (ост.)

 

Завдання 3 Перший спортсмен пробіг 820 м за 3 хв 25 с, а другий — 1658 м за 7 хв 5 с. У котрого з них більша швидкість руху?

Розв’язання

3 хв 25 с = 60 • 3 + 25 с = 205 с

7 хв 5 с = 60 • 7 + 5 = 425 с

1)_820 | 205      820    4 (м/с) – швидкість першого спортсмена.          0

2)_1658 | 425      1275    3 (м/с) – швидкість другого спортсмена.        383 (ост.)

Відповідь: більша швидкість першого спортсмена.