
ГДЗ Математика 3 клас Гісь О.М., Філяк І.В. 2016 / 2020 / 2025 рік
ГДЗ Математика 3 клас
Урок 40
Завдання 1
1) Зігни паперовий круг навпіл так, щоб обидві половинки сумістилися. Розгорни круг і подивись на лінію згину. Як її можна назвати? Діаметр
2) Зігни круг учетверо так, щоб усі 4 частини сумістилися. Розглянь лінії згину. Скільки тут радіусів? Чотири
Скільки діаметрів? Два
На скільки частин поділиться круг, якщо його ще раз зігнути навпіл? Вісім
Завдання 2
Радіуси кола: EO, AO, CO, FO, BO
Діаметри кола: AB, EF
1) У колі провести безліч радіусів. У колі можна провести безліч діаметрів
2) Всі зображені радіуси кола завжди рівні між собою. Всі діаметри кола завжди рівні між собою.
Завдання 3
Діаметр кола завжди дорівнює двом його радіусам.
Завдання 4
Діаметр більший, ніж радіус. У 2 рази.
Завдання 5
1) Радіус круглого дупла білки — 7 см. Який діаметр дупла?
7 см • 2 = 14 см
2) Діаметр виритої кротом ямки — 10 см. Який радіус цієї ямки?
10 см : 2 = 5 см
Завдання 6 Лелека накреслив коло, виміряв його радіус та діаметр і записав три схеми. Склади до них рівності, якщо діаметр кола — 18 см.
18 : 2 = 9 (см) – радіус кола
9 • 2 = 18 (см) – діаметр кола
18 – 9 = 9 (см) – на стільки сантиметрів більший діаметр (на стільки сантиметрів менший радіус)
Склади до них вирази, якщо діаметр кола — 18 см.
18 : 2, 9 • 2, 18 – 9
Завдання 7 Радіус кожного круга — 2 см.
1) 2 • 4 = 8 (см) – довжина синього відрізка
2) 2 • 4 = 8 (см) – довжина червоної ламаної лінії
3) (2 + 2) • 4 = 16 (см) – периметр зеленого квадрата
Завдання 8
56 : 8 + 16 = 23 23 – 8 + 55 = 70
(70 – 28) : 6 = 7 7 • 7 + 11 = 60
60 : (54 : 9) = 10 10 • 4 + 16 = 56
Завдання 9
1) 2 + 2 = 4 (см) – довжина сторони жовтого квадрата
2) 1 • 4 • 2 + 1 • 2 • 2 = 12 (см) – периметр синього прямокутника
3) 6 : 2 = 3 (см) – радіус сірого круга
4 : 2 = 2 (см) – радіус зеленого круга
Завдання 10 Накресли кожну фігуру, не відриваючи руки від паперу і не проводячи двічі по одній лінії.
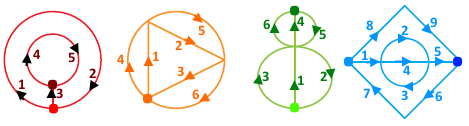
Завдання 11 Радіус зеленого круга дорівнює 5 см
1) 5 • 4 = 20 (см) – діаметр сірого круга
2) (5 • 2) • 4 = 40 (см) – периметр малого квадрата
3) (5 • 6 + 5 • 4) • 2 = 100 (см) – периметр найбільшого прямокутника